среда, 10 июля 2024 г.

დისპერსია (წყლის ტალღები)

ცოდნა სინათლეა - Knowledge is light - Знание свет -  

            დისპერსია (წყლის ტალღები)
სინოსიდური ტალღა

სითხის დინამიკაში წყლის ტალღების დისპერსია ჩვეულებრივ ეხება სიხშირის დისპერსიას , რაც ნიშნავს, რომ სხვადასხვა ტალღის სიგრძის ტალღები მოძრაობენ სხვადასხვა ფაზის სიჩქარით . წყლის ტალღები, ამ კონტექსტში, არის ტალღები, რომლებიც ვრცელდება წყლის ზედაპირზე , გრავიტაციით და ზედაპირული დაძაბულობით, როგორც აღმდგენი ძალები . შედეგად, თავისუფალი ზედაპირის მქონე წყალი ზოგადად განიხილება როგორც დისპერსიული საშუალება .


წყლის გარკვეული სიღრმისთვის ზედაპირული გრავიტაციული ტალღები - ანუ ტალღები, რომლებიც წარმოიქმნება ჰაერ-წყლის ინტერფეისზე და გრავიტაცია, როგორც ერთადერთი ძალა, რომელიც აღადგენს მას სიბრტყეს - ტალღის სიგრძის მატებასთან ერთად უფრო სწრაფად ვრცელდება . მეორეს მხრივ, მოცემული (ფიქსირებული) ტალღის სიგრძისთვის, ღრმა წყალში გრავიტაციულ ტალღებს უფრო დიდი ფაზის სიჩქარე აქვს , ვიდრე ზედაპირულ წყალში .  გრავიტაციული ტალღების ქცევისგან განსხვავებით, კაპილარული ტალღები (ანუ მხოლოდ ზედაპირული დაძაბულობის გამო) უფრო სწრაფად ვრცელდება მოკლე ტალღების სიგრძეზე.


სიხშირის დისპერსიის გარდა, წყლის ტალღები ასევე ავლენენ ამპლიტუდის დისპერსიას. ეს არის არაწრფივი ეფექტი, რომლის მიხედვითაც უფრო დიდი ამპლიტუდის ტალღებს აქვთ განსხვავებული ფაზის სიჩქარე მცირე ამპლიტუდის ტალღებისგან.

სიხშირის დისტერსიული ზედაპირული გრავიტაციული ტალრებისთვის

ეს განყოფილება ეხება სიხშირის დისპერსიას ტალღებისთვის სითხის შრეზე, რომელიც იძულებულია გრავიტაციით და ხაზოვანი თეორიის მიხედვით. ზედაპირული დაძაბულობის ეფექტი სიხშირის დისპერსიაზე იხილეთ ზედაპირული დაძაბულობის ეფექტები ჰაეროვანი ტალღის თეორიაში და კაპილარული ტალღაში.

ტალრების გავრცელება და დისპერსია

უცვლელი ფორმის უმარტივესი გამავრცელებელი ტალღა არის სინუსუსური ტალღა . სინუსუსური ტალღა წყლის ზედაპირის სიმაღლით η ( x , t ) მოცემულია: 

{\displaystyle \eta (x,t)=a\sin \left(\theta (x,t)\right),\,}

სადაც a არის ამპლიტუდა (მეტრებში) და θ = θ ( x , t ) არის ფაზის ფუნქცია ( რადიანებში ), ჰორიზონტალურ მდგომარეობაზე ( x , მეტრებში) და დროზე ( t , წამებში ) დამოკიდებულია: [3]

{\displaystyle \theta =2\pi \left({\frac {x}{\lambda }}-{\frac {t}{T}}\right)=kx-\omega t,}თან {\displaystyle k={\frac {2\pi }{\lambda }}}და {\displaystyle \omega ={\frac {2\pi }{T}},}

სადაც:

წყლის ტალღის დამახასიათებელი ფაზებია:

  • აღმავალი ნულოვანი გადაკვეთა θ = 0 -ზე ,
  • ტალღის ქერქი θ =  -ზე1/2 π ,
  • დაღმავალი ნულოვანი გადაკვეთა θ = π და
  • ტალღის ღერო θ =  1  - ზე+1/2 პ.

გარკვეული ფაზა მეორდება 2π- ის მთელი რიცხვი m ჯერადის შემდეგ : sin( θ ) = sin( θ+m•2π ).

წყლის ტალღებისთვის და ფიზიკაში ტალღის სხვა ფენომენებისთვის მნიშვნელოვანია ის , რომ თავისუფალი გავრცელების ტალღები, რომლებიც არ არის ნულოვანი ამპლიტუდისა, არსებობს მხოლოდ მაშინ, როდესაც კუთხური სიხშირე ω და ტალღის რიცხვი k (ან ექვივალენტურად ტალღის სიგრძე λ და პერიოდი T ) აკმაყოფილებს ფუნქციურ ურთიერთობას : სიხშირის დისპერსიას. კავშირი 

{\displaystyle \omega ^{2}=\Omega ^{2}(k).\,}

დისპერსიულ მიმართებას აქვს ორი ამონახსნი: ω = +Ω(k) და ω = −Ω(k) , რაც შეესაბამება ტალღებს, რომლებიც მოძრაობენ დადებითი ან უარყოფითი x – მიმართულებით. დისპერსიული კავშირი ზოგადად დამოკიდებული იქნება რამდენიმე სხვა პარამეტრზე გარდა k ტალღის რიცხვისა . გრავიტაციული ტალღებისთვის, ხაზოვანი თეორიის მიხედვით, ეს არის აჩქარება გრავიტაციით g და წყლის სიღრმე h . ამ ტალღების დისპერსიული კავშირი არის: 

{\displaystyle \omega ^{2}=g\,k\,\tanh(k\,h)}  ან  {\displaystyle \displaystyle \lambda ={\frac {g}{2\pi }}\,T^{2}\,\tanh \left(2\pi \,{\frac {h}{\lambda }}\right),}

იმპლიციტური განტოლება tanh-ით, რომელიც აღნიშნავს ჰიპერბოლური ტანგენტის ფუნქციას.

საწყისი ტალღის ფაზა θ = θ 0 ვრცელდება სივრცისა და დროის ფუნქციის მიხედვით . მისი შემდგომი პოზიცია მოცემულია:

{\displaystyle x={\frac {\lambda }{T}}\,t+{\frac {\lambda }{2\pi }}\,\theta _{0}={\frac {\omega }{k}}\,t+{\frac {\theta _{0}}{k}}.}

ეს აჩვენებს, რომ ფაზა მოძრაობს სიჩქარით: [2]

{\displaystyle c_{p}={\frac {\lambda }{T}}={\frac {\omega }{k}}={\frac {\Omega (k)}{k}},}

რომელსაც ფაზის სიჩქარეს უწოდებენ.

ფაზის სიჩქარე

რედაქტირება
დამატებითი ინფორმაცია: ფაზის სიჩქარე
გრავიტაციული ტალღების დისპერსია სითხის ზედაპირზე. ფაზის და ჯგუფის სიჩქარე დაყოფილია არაღრმა წყლის ფაზის სიჩქარეზე √ gh ფარდობითი სიღრმის h / λ ფუნქციის მიხედვით .
ლურჯი ხაზები (A): ფაზის სიჩქარე; წითელი ხაზები (B): ჯგუფური სიჩქარე; შავი წყვეტილი ხაზი (C): ფაზა და ჯგუფის სიჩქარე √ gh მოქმედებს არაღრმა წყალში.
დახატული ხაზები: დისპერსიული კავშირი მოქმედებს თვითნებურ სიღრმეში.
წყვეტილი ხაზები (ლურჯი და წითელი): ღრმა წყლის საზღვრები.
გრავიტაციული ტალღების დისპერსია სითხის ზედაპირზე. ფაზის და ჯგუფის სიჩქარე გაყოფილი ღრმა წყლის ფაზის სიჩქარეზე √ gλ  / (2 π ) ფარდობითი სიღრმის h  /  λ ფუნქციის მიხედვით .
ლურჯი ხაზები (A): ფაზის სიჩქარე; წითელი ხაზები (B): ჯგუფური სიჩქარე; შავი წყვეტილი ხაზი (C): ფაზა და ჯგუფის სიჩქარე √ gh მოქმედებს არაღრმა წყალში.
დახატული ხაზები: დისპერსიული კავშირი მოქმედებს თვითნებურ სიღრმეში.
წყვეტილი ხაზები (ლურჯი და წითელი): ღრმა წყლის საზღვრები.

სინუსოიდური ტალღა, ზედაპირის სიმაღლის მცირე ამპლიტუდისა და მუდმივი ტალღის სიგრძით , ვრცელდება ფაზის სიჩქარით , რომელსაც ასევე უწოდებენ სისწრაფეს ან ფაზის სიჩქარეს. მიუხედავად იმისა, რომ ფაზის სიჩქარე არის ვექტორი და აქვს დაკავშირებული მიმართულება, სისწრაფე ან ფაზის სიჩქარე ეხება მხოლოდ ფაზის სიჩქარის სიდიდეს. ხაზოვანი თეორიის თანახმად, ტალღების იძულებითი სიმძიმის მიხედვით, ფაზის სიჩქარე დამოკიდებულია ტალღის სიგრძეზე და წყლის სიღრმეზე. წყლის ფიქსირებული სიღრმისთვის გრძელი ტალღები (დიდი ტალღის სიგრძით) უფრო სწრაფად ვრცელდება, ვიდრე მოკლე ტალღები.

მარცხენა ფიგურაში ჩანს, რომ არაღრმა წყლის ტალღები, ტალღის სიგრძით λ ბევრად აღემატება წყლის სიღრმეს h , მოძრაობს ფაზის სიჩქარით 

{\displaystyle c_{p}={\sqrt {gh}}\qquad \scriptstyle {\text{(shallow water),}}\,}

g გრავიტაციით აჩქარებით და c p ფაზის სიჩქარით . ვინაიდან ეს არაღრმა წყლის ფაზის სიჩქარე ტალღის სიგრძისგან დამოუკიდებელია, არაღრმა წყლის ტალღებს არ გააჩნია სიხშირის დისპერსია.

სხვა ნორმალიზების გამოყენებით იგივე სიხშირის დისპერსიული ურთიერთობისთვის, ფიგურა მარჯვნივ გვიჩვენებს, რომ ფიქსირებული ტალღის სიგრძისთვის λ ფაზის სიჩქარე c p იზრდება წყლის სიღრმის მატებასთან ერთად. [1] სანამ ღრმა წყალში, რომლის სიღრმე h ტალღის ნახევარზე მეტია λ (ასე რომ h/λ > 0,5 ), ფაზის სიჩქარე c p დამოუკიდებელია წყლის სიღრმეზე: [2]

{\displaystyle c_{p}={\sqrt {\frac {g\lambda }{2\pi }}}={\frac {g}{2\pi }}T\qquad \scriptstyle {\text{(deep water),}}}

T- ით ტალღის პერიოდი ( f , T=1/f სიხშირის ორმხრივი ) . ასე რომ, ღრმა წყალში ფაზის სიჩქარე იზრდება ტალღის სიგრძესთან და პერიოდთან ერთად.

ვინაიდან ფაზის სიჩქარე აკმაყოფილებს cp = λ /T = λf , ტალღის სიგრძე და პერიოდი (ან სიხშირე) დაკავშირებულია. მაგალითად ღრმა წყალში:

{\displaystyle \lambda ={\frac {g}{2\pi }}T^{2}\qquad \scriptstyle {\text{(deep water).}}}

დისპერსიის მახასიათებლები შუალედური სიღრმისთვის მოცემულია ქვემოთ.

ჯგუფური სიჩქარე

რედაქტირება
დამატებითი ინფორმაცია: ჯგუფური სიჩქარე
სიხშირის დისპერსია გრავიტაციული ტალღების ბიქრომატულ ჯგუფებში ღრმა წყლის ზედაპირზე. წითელი კვადრატი მოძრაობს ფაზის სიჩქარით , ხოლო მწვანე წრეები ჯგუფური სიჩქარით ვრცელდება.

ორი სინუსოიდური ტალღის ჩარევა ოდნავ განსხვავებული ტალღის სიგრძით, მაგრამ იგივე ამპლიტუდა და გავრცელების მიმართულება, იწვევს ტალღის ჯგუფს. როგორც ანიმაციაში ჩანს, ჯგუფი მოძრაობს ჯგუფური სიჩქარით c g განსხვავებული ფაზის სიჩქარისგან c p , სიხშირის დისპერსიის გამო.

ჯგუფის სიჩქარე გამოსახულია წითელი ხაზებით (მონიშნული B ) ზემოთ მოცემულ ორ ფიგურაში. არაღრმა წყალში ჯგუფის სიჩქარე უდრის ზედაპირული წყლის ფაზის სიჩქარეს. ეს იმიტომ ხდება, რომ ზედაპირული წყლის ტალღები არ არის დისპერსიული. ღრმა წყალში ჯგუფის სიჩქარე უდრის ფაზის სიჩქარის ნახევარს: {{მათემატიკა| c g = 1/2გ პ . 

ჯგუფური სიჩქარე ასევე აღმოჩნდება ენერგიის ტრანსპორტირების სიჩქარე. ეს არის სიჩქარე, რომლითაც საშუალო ტალღის ენერგია ჰორიზონტალურად ტრანსპორტირდება ვიწროზოლიანი ტალღის ველში. 

ფაზური სიჩქარისგან განსხვავებული ჯგუფის სიჩქარის შემთხვევაში, შედეგი არის ის, რომ ტალღების ჯგუფში დათვლილი ტალღების რაოდენობა განსხვავებულია, როდესაც დათვლილია სივრცეში გადაღებული სურათიდან გარკვეულ მომენტში, ვიდრე დროში დათვლილი ზედაპირის გაზომილი სიმაღლიდან. ფიქსირებულ პოზიციაზე. განვიხილოთ Λ g სიგრძის ტალღის ჯგუფი და τ g ხანგრძლივობის ჯგუფი . ჯგუფის სიჩქარეა: 

{\displaystyle c_{g}={\frac {\Lambda _{g}}{\tau _{g}}}.}
ტალღების რაოდენობა თითო ჯგუფზე, როგორც დაფიქსირდა სივრცეში გარკვეულ მომენტში (ზედა ლურჯი ხაზი), განსხვავდება ტალღების რაოდენობაზე თითო ჯგუფზე, რომელიც დროში ჩანს ფიქსირებულ პოზიციაზე (ქვედა ნარინჯისფერი ხაზი), სიხშირის დისპერსიის გამო.
ჩრდილოეთ წყნარი ოკეანის ქარიშხლის ტალღები, როგორც ჩანს NOAA M/V კეთილშობილური ვარსკვლავიდან, ზამთარი 1989 წ.

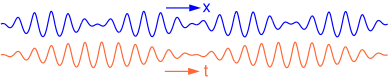
ტალღების ჯგუფში ტალღების რაოდენობა, რომელიც იზომება სივრცეში გარკვეულ მომენტში არის: Λ g  / λ . დროში ფიქსირებულ ადგილას გაზომვისას, ტალღების რაოდენობა ჯგუფში არის: τ g  / T. ასე რომ, სივრცეში გაზომილი ტალღების რაოდენობის თანაფარდობა დროში გაზომილ ტალღებთან არის:

{\displaystyle {\tfrac {\text{No. of waves in space}}{\text{No. of waves in time}}}={\frac {\Lambda _{g}/\lambda }{\tau _{g}/T}}={\frac {\Lambda _{g}}{\tau _{g}}}\cdot {\frac {T}{\lambda }}={\frac {c_{g}}{c_{p}}}.}

ასე რომ ღრმა წყალში, c g = 1/2c p , [11] ტალღების ჯგუფს აქვს ორჯერ მეტი ტალღა დროში, ვიდრე სივრცეში. [12]

წყლის ზედაპირის სიმაღლე η(x,t) , როგორც ფუნქცია x ჰორიზონტალური პოზიციისა და დროის t , სრული მოდულაციის ორქრომატული ტალღის ჯგუფისთვის შეიძლება მათემატიკურად ჩამოყალიბდეს როგორც: 

{\displaystyle \eta =a\,\sin \left(k_{1}x-\omega _{1}t\right)+a\,\sin \left(k_{2}x-\omega _{2}t\right),}

ერთად:

ორივე ω 1 და k 1 , ისევე როგორც ω 2 და k 2 , უნდა აკმაყოფილებდეს დისპერსიულ მიმართებას:

{\displaystyle \omega _{1}^{2}=\Omega ^{2}(k_{1})\,}და {\displaystyle \omega _{2}^{2}=\Omega ^{2}(k_{2}).\,}

ტრიგონომეტრიული იდენტობების გამოყენებით , ზედაპირის სიმაღლე იწერება როგორც: 

{\displaystyle \eta =\left[2\,a\,\cos \left({\frac {k_{1}-k_{2}}{2}}x-{\frac {\omega _{1}-\omega _{2}}{2}}t\right)\right]\;\cdot \;\sin \left({\frac {k_{1}+k_{2}}{2}}x-{\frac {\omega _{1}+\omega _{2}}{2}}t\right).}

კვადრატულ ფრჩხილებს შორის ნაწილი არის ჯგუფის ნელ-ნელა ცვალებადი ამპლიტუდა, ჯგუფის ტალღის ნომრით 1/2 ( k 1  − k 2  ) და ჯგუფის კუთხური სიხშირე 1/2 ( ω 1  − ω 2  ) . შედეგად, ჯგუფის სიჩქარე არის k 1  → k 2 ზღვრისთვის  : 

{\displaystyle c_{g}=\lim _{k_{1}\,\to \,k_{2}}{\frac {\omega _{1}-\omega _{2}}{k_{1}-k_{2}}}=\lim _{k_{1}\,\to \,k_{2}}{\frac {\Omega (k_{1})-\Omega (k_{2})}{k_{1}-k_{2}}}={\frac {{\text{d}}\Omega (k)}{{\text{d}}k}}.}

ტალღების ჯგუფების ამოცნობა შესაძლებელია მხოლოდ ვიწრო ზოლიანი სიგნალის შემთხვევაში, ტალღის რიცხვის სხვაობით k 1  − k 2 მცირე ტალღის საშუალო რიცხვთან შედარებით. 1/2 (k 1  + k 2 ) .

მრავალკომპონენტიანი ტალღის შაბლონები

რედაქტირება
ზედაპირული გრავიტაციული ტალღების სიხშირის დისპერსია ღრმა წყალზე. ნაჩვენებია სამი სინუსოიდური ტალღის კომპონენტის სუპერპოზიცია (მუქი ლურჯი ხაზი) ​​(ღია ლურჯი ხაზები ) .

სიხშირის დისპერსიის ეფექტი არის ის, რომ ტალღები მოძრაობენ ტალღის სიგრძის ფუნქციით, ასე რომ, გავრცელების ტალღის სივრცითი და დროითი ფაზის თვისებები მუდმივად იცვლება. მაგალითად, გრავიტაციის გავლენის ქვეშ, უფრო გრძელი ტალღის სიგრძის წყლის ტალღები უფრო სწრაფად მოძრაობენ, ვიდრე მოკლე ტალღის სიგრძის ტალღები.

მიუხედავად იმისა, რომ ორ ზედმეტად განლაგებულ სინუსოიდულ ტალღას, რომელსაც ბიქრომატულ ტალღას უწოდებენ, აქვს კონვერტი , რომელიც უცვლელად მოძრაობს, სამი ან მეტი სინუსოიდური ტალღის კომპონენტი იწვევს ტალღების და მათი გარსის შეცვლას. ზღვის მდგომარეობა - ეს არის რეალური ტალღები ზღვაზე ან ოკეანეში - შეიძლება შეფასდეს, როგორც მრავალი სინუსოიდური ტალღების სუპერპოზიცია სხვადასხვა ტალღის სიგრძით, ამპლიტუდებით, საწყისი ფაზებით და გავრცელების მიმართულებებით. თითოეული ეს კომპონენტი მოძრაობს საკუთარი ფაზის სიჩქარით, დისპერსიული ურთიერთობის შესაბამისად. ასეთი ზედაპირის სტატისტიკა შეიძლება აღწერილი იყოს მისი სიმძლავრის სპექტრით . 

დისპერსიული კავშირი

რედაქტირება

ქვემოთ მოცემულ ცხრილში მოცემულია დისპერსიული მიმართება ω 2 = [ Ω(k) ] 2 კუთხური სიხშირე ω = 2π / T და ტალღის რიცხვს k = 2π / λ შორის , აგრეთვე ფაზის და ჯგუფის სიჩქარეები. 

გრავიტაციული ტალღების სიხშირის დისპერსია ღრმა წყლის ზედაპირზე, არაღრმა და შუალედურ სიღრმეზე, ხაზოვანი ტალღების თეორიის მიხედვით
რაოდენობასიმბოლოერთეულებიღრმა წყალი
( h > 1/2 λ )		არაღრმა წყალი
( სთ < 0,05 λ )		შუალედური სიღრმე
(ყველა λ და h )
დისპერსიული კავშირი{\displaystyle \displaystyle \Omega (k)}რად /ს{\displaystyle {\sqrt {gk}}={\sqrt {\frac {2\pi \,g}{\lambda }}}}{\displaystyle k{\sqrt {gh}}={\frac {2\pi }{\lambda }}{\sqrt {gh}}}{\displaystyle {\begin{aligned}&{\sqrt {gk\,\tanh \left(kh\right)}}\,\\[1.2ex]&={\sqrt {{\frac {2\pi g}{\lambda }}\tanh \left({\frac {2\pi h}{\lambda }}\right)}}\,\end{aligned}}}
ფაზის სიჩქარე{\displaystyle \displaystyle c_{p}={\frac {\lambda }{T}}={\frac {\omega }{k}}}ქალბატონი{\displaystyle {\sqrt {\frac {g}{k}}}={\frac {g}{\omega }}={\frac {g}{2\pi }}T}{\displaystyle {\sqrt {gh}}}{\displaystyle {\sqrt {{\frac {g}{k}}\tanh \left(kh\right)}}}
ჯგუფური სიჩქარე{\displaystyle \displaystyle c_{g}={\frac {\partial \Omega }{\partial k}}}ქალბატონი{\displaystyle {\frac {1}{2}}{\sqrt {\frac {g}{k}}}={\frac {1}{2}}{\frac {g}{\omega }}={\frac {g}{4\pi }}T}{\displaystyle {\sqrt {gh}}}{\displaystyle {\frac {1}{2}}c_{p}\left(1+{\frac {2kh}{\sinh \left(2kh\right)}}\right)}
თანაფარდობა{\displaystyle \displaystyle {\frac {c_{g}}{c_{p}}}}-{\displaystyle \displaystyle {\frac {1}{2}}}{\displaystyle \displaystyle 1}{\displaystyle {\frac {1}{2}}\left(1+{\frac {2kh}{\sinh \left(2kh\right)}}\right)}
ტალღის სიგრძე{\displaystyle \displaystyle \lambda }მ{\displaystyle {\frac {g}{2\pi }}T^{2}}{\displaystyle T{\sqrt {gh}}}მოცემული T პერიოდისთვის , ამონახსნი:
 
{\displaystyle \displaystyle \left({\frac {2\pi }{T}}\right)^{2}={\frac {2\pi g}{\lambda }}\tanh \left({\frac {2\pi h}{\lambda }}\მარჯვნივ)}

ღრმა წყალი შეესაბამება წყლის სიღრმეს, რომელიც აღემატება ტალღის სიგრძის ნახევარს , რაც ჩვეულებრივი სიტუაციაა ოკეანეში. ღრმა წყალში, უფრო გრძელი პერიოდის ტალღები უფრო სწრაფად ვრცელდება და უფრო სწრაფად ატარებს მათ ენერგიას. ღრმა წყლის ჯგუფის სიჩქარე არის ფაზის სიჩქარის ნახევარი . არაღრმა წყალში , წყლის სიღრმეზე ოცჯერ მეტი ტალღის სიგრძისთვის,  როგორც საკმაოდ ხშირად გვხვდება სანაპიროსთან ახლოს, ჯგუფის სიჩქარე უდრის ფაზის სიჩქარეს.

ისტორია

რედაქტირება

სრული წრფივი დისპერსიის მიმართება პირველად აღმოაჩინა პიერ-სიმონ ლაპლასმა , თუმცა იყო გარკვეული შეცდომები ხაზოვანი ტალღის პრობლემის გადაწყვეტაში. წყლის ხაზოვანი ტალღების სრული თეორია, დისპერსიის ჩათვლით, მიღებული იქნა ჯორჯ ბიდელ აირის მიერ და გამოქვეყნდა დაახლოებით 1840 წელს. ანალოგიური განტოლება იპოვა ფილიპ კელანდმაც დაახლოებით იმავე დროს (მაგრამ დაუშვა გარკვეული შეცდომები ტალღის თეორიის წარმოშობაში). . 

არაღრმა წყლის (მცირე h / λ ) ლიმიტი, ω 2 = gh k 2 , მიღებული იქნა ჯოზეფ ლუი ლაგრანჟის მიერ .

ზედაპირული დაძაბულობის ეფექტები

რედაქტირება
დამატებითი ინფორმაცია: კაპილარული ტალღა
გრავიტაციულ-კაპილარული ტალღების დისპერსია ღრმა წყლის ზედაპირზე. ფაზის და ჯგუფის სიჩქარე გაყოფილი {\displaystyle \scriptstyle {\sqrt[{4}]{g\sigma /\rho }}}შებრუნებული ფარდობითი ტალღის სიგრძის ფუნქციით {\displaystyle \scriptstyle {\frac {1}{\lambda }}{\sqrt {\sigma /(\rho g)}}}.
ლურჯი ხაზები (A): ფაზის სიჩქარე, წითელი ხაზები (B): ჯგუფის სიჩქარე.
დახატული ხაზები: დისპერსიული კავშირი გრავიტაციულ-კაპილარული ტალღებისთვის.
წყვეტილი ხაზები: დისპერსიული კავშირი ღრმა წყლის გრავიტაციული ტალღებისთვის.
წერტილოვანი ხაზები: დისპერსიული კავშირი მოქმედებს ღრმა წყლის კაპილარული ტალღებისთვის.

გრავიტაციულ-კაპილარული ტალღების შემთხვევაში, სადაც ზედაპირული დაძაბულობა გავლენას ახდენს ტალღებზე, დისპერსიული მიმართება ხდება: [5]

{\displaystyle \omega ^{2}=\left(gk+{\frac {\sigma }{\rho }}k^{3}\right)\tanh(kh),}

σ ზედაპირული დაჭიმვით (N/m) .

წყალი-ჰაერის ინტერფეისისთვის ( σ = 0,074 ნ/მ და ρ = 1000 კგ/მ 3 ) ტალღები შეიძლება მიახლოებული იყოს როგორც სუფთა კაპილარული ტალღები - დომინირებს ზედაპირული დაძაბულობის ეფექტები - ტალღების სიგრძეზე ნაკლები 0,4 სმ (0,2 დიუმი) . 7 სმ-ზე (3 ინჩზე) ტალღების სიგრძისთვის ტალღები კარგ მიახლოებას შეესაბამება სუფთა ზედაპირის გრავიტაციულ ტალღებს ძალიან მცირე ზედაპირული დაძაბულობის ეფექტებით. 

ინტერფეისური ტალღები

რედაქტირება
ტალღური მოძრაობა ინტერფეისზე სხვადასხვა სიმკვრივის უხილავი ერთგვაროვანი სითხეების ორ ფენას შორის, შემოიფარგლება ჰორიზონტალურ ხისტ საზღვრებს შორის (ზედა და ქვედა). მოძრაობა იძულებულია გრავიტაციით. ზედა ფენას აქვს საშუალო სიღრმე h და სიმკვრივე ρ , ხოლო ქვედა ფენას აქვს საშუალო სიღრმე h და სიმკვრივე ρ . ტალღის ამპლიტუდა არის a , ტალღის სიგრძე აღინიშნება λ- ით .

სითხეების ორი ერთგვაროვანი ფენისთვის, საშუალო სისქის h ინტერფეისის ქვემოთ და h ′ ზემოთ – გრავიტაციის მოქმედების ქვეშ და შემოსაზღვრული ზევით და ქვევით ჰორიზონტალური ხისტი კედლებით – მოცემულია დისპერსიული ურთიერთობა ω 2  = Ω 2 ( k ) გრავიტაციული ტალღებისთვის. ავტორი: 

{\displaystyle \Omega ^{2}(k)={\frac {g\,k(\rho -\rho ')}{\rho \,\coth(kh)+\rho '\,\coth(kh ')}},}

სადაც ისევ ρ და ρ ′ არის სიმკვრივეები ინტერფეისის ქვემოთ და ზემოთ, ხოლო coth არის ჰიპერბოლური კოტანგენტური ფუნქცია. იმ შემთხვევაში, თუ ρ ′ არის ნული, ეს ამცირებს ზედაპირული გრავიტაციული ტალღების დისპერსიულ მიმართებას სასრული სიღრმის h წყალზე .

როდესაც ორი სითხის ფენის სიღრმე ხდება ძალიან დიდი ( h →∞, h ∞ →∞), ზემოთ მოცემულ ფორმულაში ჰიპერბოლური კოტანგენტები უახლოვდება ერთის მნიშვნელობას. შემდეგ:

{\displaystyle \Omega ^{2}(k)={\frac {\rho -\rho '}{\rho +\rho '}}\,g\,k.}

არაწრფივი ეფექტები

რედაქტირება

Ზედაპირული წყლის

რედაქტირება
დამატებითი ინფორმაცია: კნოიდური ტალღა

ამპლიტუდის დისპერსიული ეფექტები ჩნდება მაგალითად მარტოხელა ტალღაში : წყლის ერთი კეხი, რომელიც მოძრაობს მუდმივი სიჩქარით არაღრმა წყალში ჰორიზონტალური კალაპოტით. გაითვალისწინეთ, რომ მარტოხელა ტალღები თითქმის სოლიტონებია , მაგრამ არა ზუსტად - ორი (შეჯახება ან გასწრება) მარტოხელა ტალღის ურთიერთქმედების შემდეგ, ისინი ოდნავ შეიცვალა ამპლიტუდაში და რხევითი ნარჩენი დარჩა.  კორტევეგ-დე ვრის განტოლების ერთჯერადი სოლიტონის ამონახსნი , H ტალღის სიმაღლე წყლის სიღრმეში h ტალღის მწვერვალიდან შორს, მოძრაობს სიჩქარით:

{\displaystyle c_{p}=c_{g}={\sqrt {g(h+H)}}.}

ასე რომ, ამ არაწრფივი გრავიტაციული ტალღისთვის ეს არის წყლის მთლიანი სიღრმე ტალღის თხემის ქვეშ, რომელიც განსაზღვრავს სიჩქარეს, უფრო მაღალი ტალღები უფრო სწრაფად მოძრაობენ, ვიდრე ქვედა ტალღები. გაითვალისწინეთ, რომ მარტოხელა ტალღური ხსნარები არსებობს მხოლოდ H- ის დადებითი მნიშვნელობებისთვის , დეპრესიის მარტოხელა გრავიტაციული ტალღები არ არსებობს.

Ღრმა წყალი

რედაქტირება
დამატებითი ინფორმაცია: Stokes wave

წრფივი დისპერსიული მიმართება - ტალღის ამპლიტუდაზე გავლენას არ ახდენს - არაწრფივი ტალღებისთვის ასევე სწორია პერტურბაციის თეორიის გაფართოების მეორე რიგის დროს, ტალღის ციცაბო კა- ს მიხედვით (სადაც a არის ტალღის ამპლიტუდა ). მესამე რიგის და ღრმა წყლისთვის, დისპერსიული კავშირი არის 

{\displaystyle \omega ^{2}=gk\left[1+(ka)^{2}\right],}  ისე  {\displaystyle c_{p}={\sqrt {\frac {g}{k}}}\,\left[1+{\tfrac {1}{2}}\,(ka)^{2}\მარჯვნივ ]+{\mathcal {O}}\left((ka)^{4}\მარჯვნივ).}

ეს ნიშნავს, რომ დიდი ტალღები უფრო სწრაფად მოძრაობენ, ვიდრე ერთი და იგივე სიხშირის პატარა. ეს შესამჩნევია მხოლოდ მაშინ, როდესაც ტალღის ციცაბო კა დიდია.

ტალღები საშუალო დენზე: დოპლერის ცვლა

რედაქტირება

წყლის ტალღები საშუალო ნაკადზე (ასე რომ, ტალღა მოძრავ გარემოში) განიცდის დოპლერის ცვლას . დავუშვათ, დისპერსიული მიმართება არამძრავი გარემოსთვის არის:

{\displaystyle \omega ^{2}=\Omega ^{2}(k),\,}

k ტალღის რიცხვით . შემდეგ საშუალო სიჩქარის ვექტორით V , დისპერსიული ურთიერთობა დოპლერის ცვლასთან ხდება: 

{\displaystyle \left(\omega -\mathbf {k} \cdot \mathbf {V} \right)^{2}=\Omega ^{2}(k),}

სადაც k არის ტალღური რიცხვის ვექტორი, რომელიც დაკავშირებულია k- თან , როგორც: k = | k |. წერტილოვანი ნამრავლი k • V უდრის: k • V = kV cos α , V- ით საშუალო სიჩქარის ვექტორის სიგრძე V : V = | V |. და α კუთხე ტალღის გავრცელების მიმართულებასა და დინების საშუალო მიმართულებას შორის. ტალღებისა და დენისთვის ერთი და იგივე მიმართულებით k • V = kV .

იხ. ვიდეო - Фазовая скорость против групповой скорости: волновая дисперсия



на

Комментариев нет:

Отправить комментарий

Подписаться на: Комментарии к сообщению (Atom)

ანწლი (გვარი)

ცოდნა სინათლეა - Knowledge is light - Знание свет -                             ანწლი (გვარი) ანწლი  ( ლათ.   Sambucus ) —  ყვავილოვან მცენ...

  • გეოგლიფი
                                  გეოგლიფი                            ისტორიამდელი  უფინგტონის თეთრი ცხენი  — ევროპის ყველაზე ცნობილი გეოგლ...
  • აფრო-ამერიკელები
    ცოდნა სინათლეა - Knowledge is light - Знание свет -                            აფრო-ამერიკელები აფრო-მარეკილების ჯგუფი 1905-10წწ  არიან  ამ...
  • ევკარიოტები
                               ევკარიოტები                                                               ჩვენ ვიკვლევთ სიცოცხლის წარმოშობი...