შოთას ბლოგი: შავი ხვრელის საინფორმაციო პარადოქსი

ცოდნა სინათლეა - Knowledge is light - Знание свет -

შავი ხვრელის საინფორმაციო პარადოქსი

შავი ხვრელის პირველი სურათი (სილუეტი ან ჩრდილი), რომელიც M87-ის სუპერმასიურ შავ ხვრელს Event Horizon Telescope- ით გადაუღეს , 2019 წლის აპრილში გამოქვეყნდა.

შავი ხვრელის საინფორმაციო პარადოქსი ^არის პარადოქსი , რომელიც ჩნდება კვანტური მექანიკისა და ზოგადი ფარდობითობის პროგნოზების გაერთიანების დროს . ზოგადი ფარდობითობის თეორია პროგნოზირებს შავი ხვრელების არსებობას , რომლებიც სივრცე-დროის რეგიონებია, საიდანაც არაფერი - სინათლეც კი - ვერ გამოვა. 1970-იან წლებში სტივენ ჰოკინგმა ასეთ სისტემებზე გამოიყენა კვანტური ველის თეორიის ნახევრადკლასიკური მიდგომა გამრუდებულ სივრცე-დროში და აღმოაჩინა, რომ იზოლირებული შავი ხვრელი გამოსხივების ერთ ფორმას გამოასხივებდა (ახლა მის პატივსაცემად ჰოკინგის გამოსხივებას უწოდებენ ). ის ასევე ამტკიცებდა, რომ გამოსხივების დეტალური ფორმა დამოუკიდებელი იქნებოდა შავი ხვრელის საწყისი მდგომარეობისგან და დამოკიდებული იქნებოდა მხოლოდ მის მასაზე , ელექტრულ მუხტსა და კუთხურ იმპულსზე .

ინფორმაციული პარადოქსი მაშინ ჩნდება, როდესაც განვიხილავთ პროცესს, რომლის დროსაც შავი ხვრელი ფიზიკური პროცესის მეშვეობით წარმოიქმნება და შემდეგ ჰოკინგის გამოსხივების შედეგად მთლიანად აორთქლდება. ჰოკინგის გამოთვლა ვარაუდობს, რომ გამოსხივების საბოლოო მდგომარეობა შეინარჩუნებს ინფორმაციას მხოლოდ საწყისი მდგომარეობის მთლიანი მასის, ელექტრული მუხტისა და კუთხური იმპულსის შესახებ. რადგან ბევრ სხვადასხვა მდგომარეობას შეიძლება ჰქონდეს ერთი და იგივე მასა, მუხტი და კუთხური იმპულსი, ეს იმაზე მიუთითებს, რომ მრავალი საწყისი ფიზიკური მდგომარეობა შეიძლება განვითარდეს ერთსა და იმავე საბოლოო მდგომარეობაში. ამიტომ, საწყისი მდგომარეობის დეტალების შესახებ ინფორმაცია სამუდამოდ დაიკარგება; თუმცა, ეს არღვევს როგორც კლასიკური, ასევე კვანტური ფიზიკის ძირითად პრინციპს: რომ, მხოლოდ პრინციპში, სისტემის მდგომარეობა დროის ერთ მომენტში უნდა განსაზღვრავდეს მის მდგომარეობას ნებისმიერ სხვა დროს. კერძოდ, კვანტურ მექანიკაში სისტემის მდგომარეობა კოდირებულია მისი ტალღური ფუნქციით . ტალღური ფუნქციის ევოლუცია განისაზღვრება უნიტარული ოპერატორით , ხოლო უნიტარობა გულისხმობს, რომ ტალღური ფუნქცია დროის ნებისმიერ მომენტში შეიძლება გამოყენებულ იქნას ტალღური ფუნქციის დასადგენად წარსულში ან მომავალში. 1993 წელს დონ პეიჯმა ამტკიცებდა, რომ თუ შავი ხვრელი თავდაპირველად სუფთა კვანტურ მდგომარეობაშია და უნიტარული პროცესით მთლიანად აორთქლდება, ჰოკინგის გამოსხივების ფონ ნოიმანის ენტროპია თავდაპირველად იზრდება და შემდეგ შავი ხვრელის გაქრობის შემდეგ ნულამდე მცირდება. ამას პეიჯის მრუდი ეწოდება.

ამჟამად ზოგადად ითვლება, რომ ინფორმაცია შავი ხვრელის აორთქლების დროს ინახება. ბევრი მკვლევრისთვის პეიჯის მრუდის გამოტანა შავი ხვრელის საინფორმაციო თავსატეხის ამოხსნის სინონიმია.^{: 291} თუმცა, შეხედულებები განსხვავდება იმის შესახებ, თუ ზუსტად როგორ უნდა გამოსწორდეს ჰოკინგის თავდაპირველი ნახევრადკლასიკური გაანგარიშება. ბოლო წლებში ორიგინალური პარადოქსის რამდენიმე გაფართოება იქნა შესწავლილი. ერთად აღებული, შავი ხვრელის აორთქლების შესახებ ეს თავსატეხები გავლენას ახდენს იმაზე, თუ როგორ უნდა გაერთიანდეს გრავიტაცია და კვანტური მექანიკა. საინფორმაციო პარადოქსი კვანტური გრავიტაციის კვლევის აქტიურ სფეროდ რჩება .

შესაბამისი პრინციპები

კვანტურ მექანიკაში მდგომარეობის ევოლუციას შრედინგერის განტოლება განსაზღვრავს . შრედინგერის განტოლება ემორჩილება ორ პრინციპს, რომლებიც პარადოქსისთვისაა რელევანტური - კვანტური დეტერმინიზმი , რაც ნიშნავს, რომ მოცემული აწმყო ტალღური ფუნქციის გათვალისწინებით, მისი მომავალი ცვლილებები ცალსახად განისაზღვრება ევოლუციის ოპერატორით და შექცევადობა, რაც გულისხმობს იმ ფაქტს, რომ ევოლუციის ოპერატორს აქვს შებრუნებული, რაც ნიშნავს, რომ წარსული ტალღური ფუნქციებიც უნიკალურია. ამ ორის კომბინაცია ნიშნავს, რომ ინფორმაცია ყოველთვის უნდა იყოს შენახული. ამ კონტექსტში „ინფორმაცია“ ნიშნავს მდგომარეობის ყველა დეტალს, ხოლო დებულება, რომ ინფორმაცია უნდა იყოს შენახული, ნიშნავს, რომ ადრინდელი დროის შესაბამისი დეტალები ყოველთვის შეიძლება ხელახლა აღდგეს მოგვიანებით.

_{მათემატიკურად, შროდინგერის განტოლება გულისხმობს, რომ t 1} მომენტში ტალღური ფუნქცია შეიძლება დაკავშირებული იყოს t ₂ მომენტში ტალღურ ფუნქციასთან უნიტარული ოპერატორის საშუალებით. $|\Psi (t_{1})\rangle =U(t_{1},t_{2})|\Psi (t_{2})\rangle .$ რადგან უნიტარული ოპერატორი ბიექციურია , _t2- ზე ტალღური ფუნქციის მიღება შესაძლებელია _t1- ზე ტალღური ფუნქციიდან და პირიქით.

ზემოთ აღწერილი დროითი ევოლუციის შექცევადობა მხოლოდ მიკროსკოპულ დონეზე ვრცელდება , რადგან ტალღური ფუნქცია მდგომარეობის სრულ აღწერას იძლევა. ის არ უნდა იქნას გაგებული თერმოდინამიკურ შეუქცევადობასთან . პროცესი შეიძლება შეუქცევადად გამოიყურებოდეს, თუ მხოლოდ სისტემის უხეშ მახასიათებლებს ვაკვირდებით და არა მის მიკროსკოპულ დეტალებს, როგორც ეს ჩვეულებრივ თერმოდინამიკაში ხდება . თუმცა, მიკროსკოპულ დონეზე, კვანტური მექანიკის პრინციპები გულისხმობს, რომ ყველა პროცესი სრულიად შექცევადია.

1970-იანი წლების შუა პერიოდიდან სტივენ ჰოკინგმა და ჯეიკობ ბეკენშტეინმა წამოაყენეს თეორიული არგუმენტები, რომლებიც ვარაუდობდნენ, რომ შავი ხვრელის აორთქლება კარგავს ინფორმაციას და, შესაბამისად, ეწინააღმდეგება უნიტარულობას. უმნიშვნელოვანესია, რომ ეს არგუმენტები მიკროსკოპულ დონეზე უნდა გამოეყენებინათ და მიანიშნებდნენ, რომ შავი ხვრელის აორთქლება არა მხოლოდ თერმოდინამიკურად, არამედ მიკროსკოპულადაც შეუქცევადია. ეს ეწინააღმდეგება ზემოთ აღწერილ უნიტარულობის პრინციპს და იწვევს ინფორმაციულ პარადოქსს. ვინაიდან პარადოქსი ვარაუდობდა, რომ შავი ხვრელის ფორმირებითა და აორთქლებით კვანტური მექანიკა დაირღვევოდა, ჰოკინგმა პარადოქსი ჩამოაყალიბა „გრავიტაციული კოლაფსის დროს პროგნოზირებადობის დარღვევის“ კონტექსტში.

მიკროსკოპული შეუქცევადობის არგუმენტები დასტურდებოდა ჰოკინგის მიერ იზოლირებული შავი ხვრელების მიერ გამოსხივებული გამოსხივების სპექტრის გამოთვლით. ამ გამოთვლაში გამოყენებული იყო ზოგადი ფარდობითობისა და კვანტური ველის თეორიის ჩარჩო . ჰოკინგის გამოსხივების გამოთვლა ხორციელდება შავი ხვრელის ჰორიზონტზე და არ ითვალისწინებს სივრცე-დროის გეომეტრიის უკურეაქციას; საკმარისად დიდი შავი ხვრელისთვის ჰორიზონტზე სიმრუდე მცირეა და, შესაბამისად, ორივე თეორია უნდა იყოს ვალიდური. ჰოკინგი ეყრდნობოდა „თმების გარეშე“ თეორემას, რათა მისულიყო იმ დასკვნამდე, რომ შავი ხვრელების მიერ გამოსხივებული გამოსხივება დამოკიდებული იქნებოდა მხოლოდ რამდენიმე მაკროსკოპულ პარამეტრზე, როგორიცაა შავი ხვრელის მასა, მუხტი და ბრუნვა, და არა საწყისი მდგომარეობის დეტალებზე, რამაც გამოიწვია შავი ხვრელის ფორმირება. გარდა ამისა, ინფორმაციის დაკარგვის არგუმენტი ეყრდნობოდა შავი ხვრელის სივრცე-დროის მიზეზობრივ სტრუქტურას , რაც იმაზე მიუთითებს, რომ შიგნით არსებული ინფორმაცია გავლენას არ უნდა ახდენდეს გარედან რაიმე დაკვირვებაზე, მათ შორის შავი ხვრელის მიერ გამოსხივებულ გამოსხივებაზე ჩატარებულ დაკვირვებებზე. თუ ასეა, შავი ხვრელის გარეთ არსებული სივრცე-დროის რეგიონი დაკარგავდა ინფორმაციას ინტერიერის მდგომარეობის შესახებ შავი ხვრელის აორთქლების შემდეგ, რაც გამოიწვევდა ინფორმაციის დაკარგვას.

დღეს ზოგიერთი ფიზიკოსი თვლის, რომ ჰოლოგრაფიული პრინციპი (კერძოდ, AdS/CFT დუალურობა ) აჩვენებს, რომ ჰოკინგის დასკვნა არასწორი იყო და რომ ინფორმაცია ფაქტობრივად შენარჩუნებულია. გარდა ამისა, ბოლოდროინდელი ანალიზები მიუთითებს, რომ ნახევრადკლასიკურ გრავიტაციაში ინფორმაციის დაკარგვის პარადოქსის ფორმულირება თვითთანმიმდევრულად შეუძლებელია, რადგან მისი ფორმულირებისთვის საჭირო ყველა აუცილებელი ვარაუდის ერთდროულად რეალიზების შეუძლებლობაა.

შავი ხვრელის აორთქლება

ჰოკინგის რადიაცია

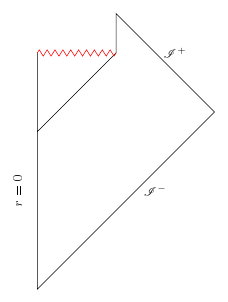
პენროუზის დიაგრამა , რომელიც ასახავს ფორმირებულ და შემდეგ მთლიანად ორთქლდება შავ ხვრელს. დრო ნაჩვენებია ვერტიკალურ ღერძზე ქვემოდან ზემოთ; სივრცე ნაჩვენებია ჰორიზონტალურ ღერძზე მარცხნიდან (ნულოვანი რადიუსი) მარჯვნივ (მზარდი რადიუსი).

1973–1975 წლებში სტივენ ჰოკინგმა აჩვენა, რომ შავი ხვრელები ნელ-ნელა უნდა გამოსხივებდნენ ენერგიას და მოგვიანებით მან დაამტკიცა, რომ ეს იწვევს უნიტარულობასთან წინააღმდეგობას. ჰოკინგმა გამოიყენა კლასიკური „ თმების გარეშე“ თეორემა იმის დასამტკიცებლად, რომ ამ გამოსხივების ფორმა - რომელსაც ჰოკინგის გამოსხივება ეწოდება - სრულიად დამოუკიდებელი იქნებოდა ვარსკვლავის ან მატერიის საწყისი მდგომარეობისგან, რომელიც კოლაფსირდა და შავი ხვრელი წარმოიქმნა. ის ამტკიცებდა, რომ გამოსხივების პროცესი გაგრძელდებოდა მანამ, სანამ შავი ხვრელი სრულად არ აორთქლდებოდა. ამ პროცესის დასასრულს, შავი ხვრელის მთელი საწყისი ენერგია გადაეცემოდა გამოსხივებას. თუმცა, ჰოკინგის არგუმენტის თანახმად, გამოსხივება არ შეინარჩუნებდა ინფორმაციას საწყისი მდგომარეობის შესახებ და, შესაბამისად, საწყისი მდგომარეობის შესახებ ინფორმაცია დაიკარგებოდა.

უფრო კონკრეტულად, ჰოკინგი ამტკიცებდა, რომ შავი ხვრელიდან გამოსხივებული გამოსხივების ნიმუში იქნებოდა შემთხვევითი, ალბათური განაწილებით, რომელიც კონტროლდება მხოლოდ შავი ხვრელის საწყისი ტემპერატურით, მუხტით და კუთხური იმპულსით და არა კოლაფსის საწყისი მდგომარეობით. ასეთი ალბათური პროცესით წარმოქმნილ მდგომარეობას კვანტურ მექანიკაში შერეული მდგომარეობა ეწოდება . ამიტომ, ჰოკინგი ამტკიცებდა, რომ თუ ვარსკვლავი ან მასალა, რომელიც კოლაფსირდა შავი ხვრელის წარმოსაქმნელად, დაიწყებოდა სპეციფიკურ სუფთა კვანტურ მდგომარეობაში , აორთქლების პროცესი სუფთა მდგომარეობას შერეულ მდგომარეობაში გარდაქმნიდა. ეს ეწინააღმდეგება ზემოთ განხილულ კვანტურ-მექანიკური ევოლუციის უნიტარულობას.

ინფორმაციის დაკარგვის რაოდენობრივი განსაზღვრა შესაძლებელია მდგომარეობის წვრილმარცვლოვანი ფონ ნოიმანის ენტროპიის ცვლილების თვალსაზრისით. სუფთა მდგომარეობას ენიჭება 0 ფონ ნოიმანის ენტროპია, ხოლო შერეულ მდგომარეობას აქვს სასრული ენტროპია. შროდინგერის განტოლების მიხედვით მდგომარეობის უნიტარული ევოლუცია ინარჩუნებს ენტროპიას. ამიტომ, ჰოკინგის არგუმენტი ვარაუდობს, რომ შავი ხვრელის აორთქლების პროცესი არ შეიძლება აღიწეროს უნიტარული ევოლუციის ფარგლებში. მიუხედავად იმისა, რომ ეს პარადოქსი ხშირად კვანტური მექანიკის ტერმინებით არის ჩამოყალიბებული, სუფთა მდგომარეობიდან შერეულ მდგომარეობაში ევოლუცია ასევე არ შეესაბამება კლასიკურ ფიზიკაში ლიუვილის თეორემას (იხ. მაგ. ).

განტოლებებში ჰოკინგმა აჩვენა, რომ თუ ერთი აღნიშნავს შექმნისა და განადგურების ოპერატორებს სიხშირეზე $\omega$ შავი ხვრელის ფონზე გავრცელებული კვანტური ველისთვის $a_{\omega }$ და $a_{\omega }^{\dagger }$ მაშინ შავი ხვრელის კოლაფსის შედეგად წარმოქმნილ მდგომარეობაში ამ ოპერატორების ნამრავლის მოსალოდნელი მნიშვნელობა დააკმაყოფილებდა $\langle a_{\omega }a_{\omega }^{\dagger }\rangle _{\rm {hawk}}={1 \over 1-e^{-\omega /{kT}}}$ სადაც $k$ არის ბოლცმანის მუდმივა და $T$ არის შავი ხვრელის ტემპერატურა. (იხილეთ, მაგალითად, ^[ 9 ] -ის 2.2 ნაწილი ). ამ ფორმულას ორი მნიშვნელოვანი ასპექტი აქვს. პირველი ის არის, რომ გამოსხივების ფორმა დამოკიდებულია მხოლოდ ერთ პარამეტრზე, ტემპერატურაზე, მიუხედავად იმისა, რომ შავი ხვრელის საწყისი მდგომარეობა ვერ დახასიათდება ერთი პარამეტრით. მეორე, ფორმულა გულისხმობს, რომ შავი ხვრელი ასხივებს მასას სიჩქარით, რომელიც მოცემულია ${dM \over dt}=-{aT^{4}}$ სადაც $a$ არის ფუნდამენტურ მუდმივებთან დაკავშირებული მუდმივა, მათ შორის სტეფან-ბოლცმანის მუდმივასთან და შავი ხვრელის სივრცე-დროის გარკვეულ თვისებებთან, რომლებსაც მისი ნაცრისფერი სხეულის ფაქტორებს უწოდებენ .

შავი ხვრელის ტემპერატურა, თავის მხრივ, დამოკიდებულია მის მასაზე, მუხტსა და კუთხურ იმპულსზე. შვარცშილდის შავი ხვრელისთვის ტემპერატურა მოცემულია ფორმულით $T={\hbar c^{3} \over 8\pi kGM}$ ეს ნიშნავს, რომ თუ შავი ხვრელი თავდაპირველად მასით იწყებს $M_{0}$ , ის სრულად აორთქლდება პროპორციულ დროში $M_{0}^{3}$ .

ამ ფორმულების მნიშვნელოვანი ასპექტი ის არის, რომ ისინი ვარაუდობენ, რომ ამ პროცესით წარმოქმნილი რადიაციის საბოლოო აირი დამოკიდებულია მხოლოდ შავი ხვრელის ტემპერატურაზე და დამოუკიდებელია საწყისი მდგომარეობის სხვა დეტალებისგან. ეს იწვევს შემდეგ პარადოქსს. განვიხილოთ ორი განსხვავებული საწყისი მდგომარეობა, რომლებიც კოლაფსირდებიან და ქმნიან იმავე მასის შვარცშილდის შავ ხვრელს. მიუხედავად იმისა, რომ თავდაპირველად მდგომარეობები განსხვავებული იყო, რადგან შავი ხვრელების მასა (და შესაბამისად, ტემპერატურა) ერთნაირია, ისინი გამოყოფენ ერთსა და იმავე ჰოკინგის რადიაციას. როგორც კი ისინი მთლიანად აორთქლდებიან, ორივე შემთხვევაში დარჩება რადიაციის უხასიათო აირი. ეს აირი არ შეიძლება გამოყენებულ იქნას ორი საწყისი მდგომარეობის გასარჩევად და, შესაბამისად, ინფორმაცია დაიკარგა.

გვერდის მრუდი

1970-იან წლებში, იმავე პერიოდში, დონ პეიჯი სტივენ ჰოკინგის დოქტორანტი იყო. ის ეწინააღმდეგებოდა ჰოკინგის მსჯელობას, რამაც ზემოთ მოცემულ პარადოქსი გამოიწვია, თავდაპირველად CPT სიმეტრიის დარღვევის საფუძველზე . ^[ 19 ] 1993 წელს პეიჯმა ყურადღება გაამახვილა შავი ხვრელისა და მისი ჰოკინგის გამოსხივების კომბინირებულ სისტემაზე, როგორც ერთ ჩახლართულ სისტემაზე, ორნაწილიან სისტემაზე, რომელიც შავი ხვრელის აორთქლების სიცოცხლის განმავლობაში ვითარდება. სრული კვანტური ანალიზის ჩატარების უნარის არქონის გამო, მან მაინც გააკეთა მნიშვნელოვანი დაკვირვება: თუ შავი ხვრელი იწყება სუფთა კვანტურ მდგომარეობაში და მთლიანად აორთქლდება უნიტარული პროცესით , ჰოკინგის გამოსხივების ფონ ნოიმანის ენტროპია ან ჩახლართულობის ენტროპია თავდაპირველად ნულიდან იზრდება და შემდეგ უნდა შემცირდეს ნულამდე, როდესაც შავი ხვრელი, რომელშიც გამოსხივებაა ჩახლართული, მთლიანად აორთქლდება. ეს ცნობილია როგორც პეიჯის მრუდი; და დროს, რომელიც შეესაბამება მრუდის მაქსიმალურ ან ბრუნვის წერტილს, რომელიც ხდება შავი ხვრელის სიცოცხლის სიცოცხლის დაახლოებით ნახევარზე, ეწოდება პეიჯის დრო. მოკლედ რომ ვთქვათ, თუ შავი ხვრელის აორთქლება უნიტარულია, მაშინ რადიაციული ჩახლართულობის ენტროპია მიჰყვება პეიჯის მრუდს. პეიჯის დროის შემდეგ, კორელაციები ჩნდება და გამოსხივება სულ უფრო ინფორმაციულად მდიდარი ხდება.

უნიტარული შავი ხვრელის აორთქლებისთვის პეიჯის მრუდის გამოყვანის ბოლოდროინდელი პროგრესი მნიშვნელოვანი ნაბიჯია როგორც ინფორმაციული პარადოქსის გადაწყვეტის, ასევე კვანტური გრავიტაციის უნიტარულობის უფრო ზოგადი გაგებისკენ. ბევრი მკვლევარი პეიჯის მრუდის გამოყვანას შავი ხვრელის ინფორმაციული პარადოქსის ამოხსნის სინონიმად მიიჩნევს.პოპულარული კულტურა

ინფორმაციული პარადოქსი გაშუქდა პოპულარულ მედიაში და აღწერილია პოპულარულ სამეცნიერო წიგნებში. ამ გაშუქების ნაწილი გამოწვეული იყო ფართოდ გახმაურებული ფსონით , რომელიც 1997 წელს დადეს ჯონ პრესკილს , ერთი მხრივ, ჰოკინგსა და მეორე მხრივ, კიპ თორნს შორის , რომ ინფორმაცია შავ ხვრელებში არ იკარგებოდა. პარადოქსის შესახებ სამეცნიერო დებატები აღწერილია ლეონარდ სასკინდის 2008 წლის წიგნში „შავი ხვრელების ომი“ . (წიგნში ყურადღებით აღნიშნულია, რომ „ომი“ წმინდა სამეცნიერო იყო და რომ პირად დონეზე მონაწილეები მეგობრებად დარჩნენ. ) სასკინდი წერს, რომ ჰოკინგი საბოლოოდ დარწმუნდა, რომ შავი ხვრელის აორთქლება უნიტარული იყო ჰოლოგრაფიული პრინციპით , რომელიც პირველად შემოგვთავაზა ჯერარდ ტ ჰუფტმა , შემდგომ განავითარა სასკინდმა და მოგვიანებით ზუსტი სიმების თეორიის ინტერპრეტაცია მისცა AdS/CFT მიმოწერის საშუალებით. 2004 წელს ჰოკინგმა ასევე დათმო 1997 წლის ფსონი და პრესკილს ბეისბოლის ენციკლოპედია გადაუხადა, „რომლიდანაც ინფორმაციის მოძიება შესაძლებელია სურვილისამებრ“. თორნმა უარი თქვა დათმობაზე.

გადაწყვეტილებები

1997 წელს AdS/CFT შესაბამისობის წინადადების შემდეგ , ფიზიკოსებს შორის დომინანტური რწმენაა, რომ ინფორმაცია შავი ხვრელის აორთქლებისას მართლაც ინახება. ზოგადად, არსებობს ორი ძირითადი მიმდინარეობა იმის შესახებ, თუ როგორ ხდება ეს. იმ საზოგადოებაში, რომელსაც შეიძლება ფართოდ ვუწოდოთ „ სიმების თეორიის “, დომინანტური იდეა ის არის, რომ ჰოკინგის გამოსხივება არ არის ზუსტად თერმული, არამედ იღებს კვანტურ კორელაციებს, რომლებიც კოდირებს ინფორმაციას შავი ხვრელის ინტერიერის შესახებ. ეს თვალსაზრისი ბოლო დროს ფართომასშტაბიანი კვლევის საგანი გახდა და დამატებითი მხარდაჭერა მიიღო 2019 წელს, როდესაც მკვლევარებმა შეცვალეს ჰოკინგის გამოსხივების ენტროპიის გამოთვლა გარკვეულ მოდელებში და აჩვენეს, რომ გამოსხივება სინამდვილეში შავი ხვრელის ინტერიერის ორმაგია გვიანდელ პერიოდებში. თავად ჰოკინგზე გავლენა მოახდინა ამ შეხედულებამ და 2004 წელს გამოაქვეყნა ნაშრომი, რომელშიც ივარაუდა AdS/CFT შესაბამისობა და ამტკიცებდა, რომ მოვლენათა ჰორიზონტის კვანტურმა პერტურბაციებმა შეიძლება ინფორმაციის შავი ხვრელიდან გამოსვლის საშუალება მისცეს, რაც ინფორმაციის პარადოქსს გადაჭრიდა. ამ პერსპექტივიდან, მნიშვნელოვანია შავი ხვრელის მოვლენათა ჰორიზონტი და არა შავი ხვრელის სინგულარობა . GISR-ის ცნობები ამ იდეის განხორციელებას წარმოადგენს, სადაც მოვლენათა ჰორიზონტის კვანტური დარღვევა შავი ხვრელების მიკროსკოპული მდგომარეობით არის ჩანაცვლებული.

მეორე მხრივ, იმაში, რასაც ფართოდ შეიძლება ვუწოდოთ „ მარყუჟის კვანტური გრავიტაციის საზოგადოება“, დომინანტური შეხედულებაა, რომ ინფორმაციული პარადოქსის გადასაჭრელად მნიშვნელოვანია იმის გაგება, თუ როგორ წყდება შავი ხვრელის სინგულარობა. ამ სცენარებს ფართოდ უწოდებენ ნარჩენ სცენარებს, რადგან ინფორმაცია თანდათანობით არ ჩნდება, არამედ შავი ხვრელის წიაღში რჩება მხოლოდ შავი ხვრელის აორთქლების ბოლოს გამოსავლენად.

მკვლევრები ასევე იკვლევენ სხვა შესაძლებლობებს, მათ შორის კვანტური მექანიკის კანონების მოდიფიკაციას, რათა შესაძლებელი გახდეს არაუნიტარული დროის ევოლუცია.

ზოგიერთი ასეთი გადაწყვეტა ქვემოთ უფრო დეტალურად არის აღწერილი.

GISR მექანიზმის პარადოქსის გადაწყვეტა

ეს რეზოლუცია გრავიტაციით ინდუცირებულ სპონტანურ გამოსხივებას ჰოკინგის გამოსხივების ძირითად მექანიზმად მიიჩნევს, რომლის ფიზიკური ინგრედიენტებიც აშკარად ჰერმიტული ჰამილტონისეული ფორმულით არის დაწერილი.

${\begin{aligned}H&={\begin{pmatrix}w^{i}\\&w_{-}^{j}\\&&\ddots \\&&&{\scriptstyle {\it {0}}}^{\scriptscriptstyle {\it {1}}}\end{pmatrix}}+\sum _{q}\hbar \omega _{q}a_{q}^{\dagger }a_{q}+\sum _{u,v}^{|u-v|=\hbar \omega _{q}}g_{u^{n}v^{\ell }}b_{u^{n}v^{\ell }}^{\dagger }a_{q}\\g_{u\;\!\!^{n}v^{\ell }}&\propto -{\frac {\hbar }{G\{M_{u},M_{v}\}^{\mathrm {max} }}}\mathrm {Siml} \{\Psi [M_{u\;\!\!^{n}}\!(r)],\Psi [M_{v\;\!\!^{\ell }}\!(r)]\}\end{aligned}}$

მარჯვენა მხარეს პირველი წევრი შავი ხვრელების მიკროსკოპული მდგომარეობების მატრიცული წარმოდგენაა, რომელიც არ აღემატება საწყისს, თითოეული $w^{i}$ არის $w$ -ჯერ გადაგვარებული. მეორე ტერმინი აღწერს ნაწილაკების ვაკუუმურ რყევას შავი ხვრელის გარშემო. მესამე ტერმინი აკავშირებს ორს ისე, რომ თითოეული ვაკუუმური რეჟიმისთვის, რომლის ენერგია ემთხვევა შავი ხვრელის ორ მდგომარეობას შორის მასის სხვაობას, გადასვლა ხდება ამპლიტუდით, რომელიც პროპორციულია შავი ხვრელის საწყის და საბოლოო მიკროკოპულ მდგომარეობას შორის მსგავსების კოეფიციენტისა. გადასვლები უფრო მაღალი ენერგიის მდგომარეობიდან $w^{i}$ ენერგეტიკული მდგომარეობის შესამცირებლად $w_{-\cdots }^{k}$ და შებრუნებული, თანაბრად დაშვებულია ჰამილტონის დონეზე. ეს შეწყვილება ბაძავს ჯეინს-კამინგსის მოდელის ფოტონ-ატომის ურთიერთქმედებას ატომურ ფიზიკაში, ფოტონების ვექტორული პოტენციალის ჩანაცვლებით ჰოკინგის ნაწილაკების მასა-ენერგიით, ხოლო ატომებში საწყისიდან საბოლოო გადასვლების დიპოლური მომენტის ჩანაცვლებით შავი ხვრელების საწყისი და საბოლოო მდგომარეობების მსგავსების კოეფიციენტით.

GISR-ის ჰამილტონის თეორიით, აორთქლებადი შავი ხვრელის და მისი „ჰოკინგი“ ნაწილაკების ევოლუცია კონტროლდება სტანდარტული შროდინგერის განტოლებით,

$|\psi (t)\rangle =\sum _{u=w}^{0}\sum _{n=1}^{u}\sum _{\omega {}s}^{\omega +u=w}e^{-iut-i\omega {}t}c_{u\;\!\!^{n}}^{\omega {}s}(t)|u\;\!\!^{n}\otimes \omega {}s\rangle$

$i\hbar {\partial }_{t}|\psi (t)\rangle =H|\psi (t)\rangle$

სად $\omega {}s$ არის ჰოკინგის ნაწილაკების ინდექსი, რომელიც მითითებულია სრული ენერგიით $\omega$ მოკლევადიანი ევოლუციის ან ერთჯერადი კვანტური ემისიის დროს, ვიგნერ-ვისკოპფის მიახლოება საშუალებას იძლევა ვაჩვენოთ, რომ GISR-ის სპექტრი ზუსტად თერმული ტიპისაა და შესაბამისი ტემპერატურა ჰოკინგის გამოსხივების ტოლია. ხანგრძლივი ევოლუციის ან უწყვეტი კვანტური ემისიის დროს, პროცესი არათანაბარია და ხასიათდება საწყისი მდგომარეობაზე დამოკიდებული შავი ხვრელის მასის ან ტემპერატურისა და დროის მრუდით. შორს მყოფ დამკვირვებლებს შეუძლიათ საწყისი შავი ხვრელების მასის ან ტემპერატურისა და დროის მრუდიდან მიიღონ საწყისი შავი ხვრელების ინფორმაცია.

GISR-ის ჰამილტონის და ტალღური ფუნქციის აღწერა საშუალებას იძლევა შავ ხვრელსა და მის ჰოკინგის ნაწილაკებს შორის ჩახლართულობის ენტროპიის ექსპლიციტურად გამოთვლა,

$s_{BR}=-\operatorname {tr} _{B}\rho _{B}\log \rho _{B}=-tr_{R}\rho _{R}\log \rho _{R}$

$\rho _{B}=\operatorname {tr} _{R}\sum _{u=w}^{0}\sum _{n=1}^{u}\sum _{\omega {}s}^{\omega +u=w}|c_{u^{n}}^{\omega {}s}\rangle \langle c_{u^{n}}^{\omega {}s}|$

$\rho _{R}=\operatorname {tr} _{B}\sum _{u=w}^{0}\sum _{n=1}^{u}\sum _{\omega {}s}^{\omega +u=w}|c_{u^{n}}^{\omega {}s}\rangle \langle c_{u^{n}}^{\omega {}s}|$

ვინაიდან GISR-ის ჰამილტონიანი აშკარად ჰერმიტიანულია, შედეგად მიღებული ენტროპიის პირველი მზარდი და შემდეგ კლებადი მახასიათებელი ბუნებრივად მიიღება. გაანგარიშება გვეუბნება, რომ აორთქლებადი შავი ხვრელის შუალედური მდგომარეობა არ შეიძლება ჩაითვალოს დროზე დამოკიდებული მასის მქონე ნახევრადკლასიკურ ობიექტად. ამის ნაცვლად, ის უნდა განვიხილოთ, როგორც ნაწილობრივ გამოსხივებული შავი ხვრელებისა და ჰოკინგის ნაწილაკების მასის თანაფარდობის მრავალი განსხვავებული კომბინაციის სუპერპოზიცია. ლიტერატურაში ^[ 28 ]^[ 29 ] შროდინგერის კატის ტიპის აზროვნების ექსპერიმენტი შეიქმნა ამ ფაქტის საილუსტრაციოდ, სადაც საწყისი შავი ხვრელი უკავშირდება ცოცხალი კატების ჯგუფს და თითოეული ჰოკინგის ნაწილაკი კლავს ჯგუფიდან ერთ-ერთს. კვანტურ აღწერილობაში, რადგან გამოსხივებული ჰოკინგის ნაწილაკების დროისა და რაოდენობის ზუსტად განსაზღვრა შეუძლებელია, აორთქლებადი შავი ხვრელის შუალედური მდგომარეობა შეიძლება ჩაითვალოს მხოლოდ მრავალი კატის ჯგუფის სუპერპოზიციად, რომელთაგან თითოეულს განსხვავებული თანაფარდობა აქვს მკვდარი წევრების. ინფორმაციის დაკარგვის არგუმენტში ყველაზე მნიშვნელოვანი ნაკლი ამ სუპერპოზიციის უგულებელყოფაა.

პარადოქსის მცირე კორექციებით გადაწყვეტა

ეს იდეა იმაზე მიუთითებს, რომ ჰოკინგის გამოთვლა ვერ ახერხებს მცირე შესწორებების თვალყურის დევნებას, რომლებიც საბოლოოდ საკმარისია საწყისი მდგომარეობის შესახებ ინფორმაციის შესანარჩუნებლად. ეს შეიძლება განვიხილოთ, როგორც ანალოგი იმისა, რაც ხდება „დაწვის“ ჩვეულებრივი პროცესის დროს: წარმოქმნილი გამოსხივება, როგორც ჩანს, თერმულია, მაგრამ მისი დახვეწილი მახასიათებლები კოდირებს დამწვარი ობიექტის ზუსტ დეტალებს. ეს იდეა შეესაბამება შექცევადობას, როგორც ამას კვანტური მექანიკა მოითხოვს. ეს არის დომინანტური იდეა იმაში, რასაც ფართოდ შეიძლება ვუწოდოთ სიმების თეორიის მიდგომა კვანტური გრავიტაციის მიმართ.

უფრო ზუსტად, გადაწყვეტის ეს ხაზი მიუთითებს, რომ ჰოკინგის გამოთვლა ისეა გასწორებული, რომ ჰოკინგის მიერ გამოთვლილი და ზემოთ აღწერილი ორწერტილიანი კორელატორი ხდება $\langle a_{\omega }a_{\omega }^{\dagger }\rangle _{\rm {exact}}=\langle a_{\omega }a_{\omega }^{\dagger }\rangle _{\rm {hawk}}(1+\epsilon _{2})$ და უფრო მაღალი წერტილის კორელატორები ანალოგიურად კორეგირებულია $\langle a_{\omega _{1}}a_{\omega _{1}}^{\dagger }a_{\omega _{2}}a_{\omega _{2}}^{\dagger }\ldots a_{\omega _{n}}a_{\omega _{n}}^{\dagger }\rangle _{\rm {exact}}=\langle a_{\omega }a_{\omega }^{\dagger }\rangle _{\rm {hawk}}(1+\epsilon _{n})$ ზემოთ მოცემულ განტოლებებში გამოყენებულია მოკლე ნოტაცია და კორექტირების ფაქტორები $\epsilon _{i}$ შეიძლება დამოკიდებული იყოს ტემპერატურაზე, კორელაციის ფუნქციაში შემავალი ოპერატორების სიხშირეებსა და შავი ხვრელის სხვა დეტალებზე.

მალდასენამ თავდაპირველად ასეთი კორექტირება პარადოქსის მარტივი ვერსიით შეისწავლა. შემდეგ ისინი გააანალიზეს პაპადოდიმასმა და რაჯუმ , რომლებმაც აჩვენეს, რომ დაბალი წერტილის კორელატორების კორექტირება (როგორიცაა $\epsilon _{2}$ ზემოთ), რომლებიც ექსპონენციურად იყო ჩახშობილი შავი ხვრელის ენტროპიაში, საკმარისი იყო უნიტარულობის შესანარჩუნებლად და მნიშვნელოვანი კორექტივები საჭირო იყო მხოლოდ ძალიან მაღალი წერტილის კორელატორებისთვის. მექანიზმი, რომელიც საშუალებას იძლეოდა სწორი მცირე კორექტივების წარმოქმნის, თავდაპირველად პოსტულირებული იყო კვანტური გრავიტაციის ზუსტი ლოკალურობის დაკარგვის თვალსაზრისით, რათა შავი ხვრელის ინტერიერი და გამოსხივება აღწერილიყო თავისუფლების ერთი და იგივე ხარისხებით. ბოლოდროინდელი მიღწევები მიუთითებს, რომ ასეთი მექანიზმის რეალიზება შესაძლებელია ზუსტად ნახევარკლასიკური გრავიტაციის ფარგლებში და საშუალებას იძლევა ინფორმაცია გაქრეს. იხილეთ § ბოლოდროინდელი მიღწევები .

პარადოქსის Fuzzball გადაწყვეტა

ზოგიერთი მკვლევარი, განსაკუთრებით სამირ მათური , ამტკიცებდა , რომ ინფორმაციის შესანარჩუნებლად საჭირო მცირე შესწორებების მიღება შეუძლებელია შავი ხვრელის ინტერიერის ნახევრადკლასიკური ფორმის შენარჩუნებით და ამის ნაცვლად საჭიროა შავი ხვრელის გეომეტრიის მოდიფიკაცია ფუმფულა ბურთის სახით .

ფუმფულა ბურთის განმსაზღვრელი მახასიათებელია ის, რომ მას ჰორიზონტის მასშტაბით სტრუქტურა აქვს. ეს უნდა შევადაროთ შავი ხვრელის ინტერიერის, როგორც სივრცის ძირითადად უსახური რეგიონის, ტრადიციულ სურათს. საკმარისად დიდი შავი ხვრელისთვის, მოქცევითი ეფექტები შავი ხვრელის ჰორიზონტზე ძალიან მცირეა და მცირე რჩება ინტერიერში მანამ, სანამ შავი ხვრელის სინგულარობას არ მიუახლოვდება . ამიტომ, ტრადიციულ სურათში, დამკვირვებელმა, რომელიც ჰორიზონტს კვეთს, შეიძლება ვერც კი გააცნობიეროს, რომ ეს გააკეთა მანამ, სანამ სინგულარობას არ დაიწყებს მიახლოებას. ამის საპირისპიროდ, ფუმფულა ბურთის წინადადება ვარაუდობს, რომ შავი ხვრელის ჰორიზონტი ცარიელი არ არის. შესაბამისად, ის ასევე არ არის ინფორმაციულად თავისუფალი, რადგან ჰორიზონტის ზედაპირზე სტრუქტურის დეტალები ინარჩუნებს ინფორმაციას შავი ხვრელის საწყისი მდგომარეობის შესახებ. ეს სტრუქტურა ასევე გავლენას ახდენს გამავალ ჰოკინგის გამოსხივებაზე და ამით საშუალებას აძლევს ინფორმაციას ფუმფულა ბურთიდან გამოვიდეს.

Fuzzball-ის იდეას ადასტურებს მიკრომდგომარეობების გეომეტრიების სახელით ცნობილი გრავიტაციული გადაწყვეტილებების დიდი რაოდენობის არსებობა.

ფაირვოლის წინადადება შეიძლება განვიხილოთ, როგორც ბუნდოვანი ბურთის წინადადების ვარიანტი, რომელიც ამტკიცებს, რომ შავი ხვრელის ინტერიერი ჩანაცვლებულია ფაზბოულის ნაცვლად ფაზბოულით. ოპერაციულად, ბუნდოვან ბურთსა და ფაზბოულის წინადადებებს შორის განსხვავება იმაში მდგომარეობს, შავი ხვრელის ჰორიზონტზე გადამკვეთი დამკვირვებელი ხვდება თუ არა ფაზბოულის წინადადებით მიღებულ მაღალი ენერგიის მატერიას, თუ უბრალოდ ფაზბოულის წინადადებით მიღებულ დაბალი ენერგიის სტრუქტურას. ფაირვოლის წინადადება ასევე წარმოიშვა მათურის არგუმენტის შესწავლიდან, რომ მცირე შესწორებები არასაკმარისია ინფორმაციის პარადოქსის გადასაჭრელად.

Fuzzball-ისა და firewall-ის წინადადებები კითხვის ნიშნის ქვეშ დადგა ჰორიზონტის მასშტაბით სტრუქტურის გენერირების შესაბამისი მექანიზმის არარსებობის გამო.

პარადოქსის ძლიერი კვანტური ეფექტების გადაწყვეტა

შავი ხვრელის აორთქლების ბოლო ეტაპებზე კვანტური ეფექტები მნიშვნელოვანი ხდება და მათი იგნორირება შეუძლებელია. შავი ხვრელის აორთქლების ამ ფაზის ზუსტი გაგება მოითხოვს კვანტური გრავიტაციის სრულ თეორიას. შავი ხვრელებისადმი მარყუჟ-კვანტური გრავიტაციის მიდგომის ფარგლებში, ითვლება, რომ აორთქლების ამ ფაზის გაგება გადამწყვეტია ინფორმაციული პარადოქსის ამოსახსნელად.

ამ პერსპექტივის თანახმად, ჰოკინგის გამოთვლა სანდოა შავი ხვრელის აორთქლების საბოლოო ეტაპამდე, როდესაც ინფორმაცია მოულოდნელად გაქრება. ^[ 30 ]^[ 31 ]^[ 44 ]^[ 12 ] კიდევ ერთი შესაძლებლობა, რომელიც მსგავსია, არის ის, რომ შავი ხვრელის აორთქლება უბრალოდ წყდება, როდესაც შავი ხვრელი პლანკის ზომის ხდება. ასეთ სცენარებს „ნარჩენი სცენარები“ ეწოდება. ^[ 30 ]^[ 31 ]

ამ პერსპექტივის მიმზიდველი ასპექტი ის არის, რომ კლასიკური და ნახევრადკლასიკური გრავიტაციისგან მნიშვნელოვანი გადახრა მხოლოდ იმ რეჟიმშია საჭირო, რომელშიც კვანტური გრავიტაციის ეფექტების დომინირებაა მოსალოდნელი. მეორეს მხრივ, ეს იდეა გულისხმობს, რომ ინფორმაციის უეცარი გაჟონვის წინ, ძალიან პატარა შავ ხვრელს უნდა შეეძლოს ინფორმაციის თვითნებური რაოდენობის შენახვა და ძალიან დიდი რაოდენობით შინაგანი მდგომარეობები ჰქონდეს. ამიტომ, მკვლევარებმა, რომლებიც ამ იდეას მისდევენ, უნდა იზრუნონ ნარჩენების ტიპის სცენარების საერთო კრიტიკაზე, რომელიც გულისხმობს, რომ მათ შეიძლება დაარღვიონ ბეკენშტეინის ზღვარი და გამოიწვიონ ეფექტური ველის თეორიის დარღვევა ჩვეულებრივი გაფანტვის მოვლენებში ნარჩენების ვირტუალური ნაწილაკების სახით წარმოქმნის გამო.

პარადოქსისადმი რბილი თმის გადაწყვეტა

2016 წელს ჰოკინგმა , პერიმ და სტრომინგერმა აღნიშნეს, რომ შავი ხვრელები უნდა შეიცავდნენ „რბილ თმას“. ნაწილაკები, რომლებსაც არ აქვთ მოსვენების მასა, როგორიცაა ფოტონები და გრავიტონები, შეიძლება არსებობდნენ თვითნებურად დაბალი ენერგიით და მათ რბილი ნაწილაკები ეწოდებათ. რბილი თმის გარჩევადობა გულისხმობს, რომ საწყისი მდგომარეობის შესახებ ინფორმაცია ასეთ რბილ ნაწილაკებში ინახება. ასეთი რბილი თმის არსებობა ოთხგანზომილებიანი ასიმპტოტურად ბრტყელი სივრცის თავისებურებაა და შესაბამისად, პარადოქსის ეს გარჩევადობა არ ვრცელდება ანტი-დე სიტერის სივრცეში არსებულ შავ ხვრელებზე ან სხვა განზომილებების შავ ხვრელებზე.

ინფორმაცია შეუქცევადად იკარგება

თეორიული ფიზიკის საზოგადოებაში უმცირესობის შეხედულებაა, რომ ინფორმაცია ნამდვილად იკარგება შავი ხვრელების წარმოქმნისა და აორთქლების დროს. ეს დასკვნა გამომდინარეობს, თუ ვივარაუდებთ, რომ ნახევრადკლასიკური გრავიტაციისა და შავი ხვრელის სივრცე-დროის კაუზალური სტრუქტურის პროგნოზები ზუსტია.

თუმცა, ეს დასკვნა უნიტარულობის დაკარგვამდე მიგვიყვანს. ბენქსი, სასკინდი და პესკინი ამტკიცებენ, რომ ზოგიერთ შემთხვევაში უნიტარულობის დაკარგვა ასევე გულისხმობს ენერგია-იმპულსის შენახვის ან ლოკალურობის დარღვევას, მაგრამ ეს არგუმენტი შესაძლოა თავიდან ავიცილოთ სისტემებში, რომლებსაც თავისუფლების დიდი რაოდენობა აქვთ. როჯერ პენროუზის თანახმად , კვანტურ სისტემებში უნიტარულობის დაკარგვა პრობლემას არ წარმოადგენს: კვანტური გაზომვები თავისთავად უკვე არაუნიტარულია. პენროუზი ამტკიცებს, რომ კვანტური სისტემები ფაქტობრივად აღარ განვითარდება უნიტარულად, როგორც კი გრავიტაცია მოქმედებაში შევა, ზუსტად ისე, როგორც შავ ხვრელებში. კონფორმული ციკლური კოსმოლოგია, რომელსაც პენროუზი უჭერს მხარს, კრიტიკულად არის დამოკიდებული იმ პირობაზე, რომ ინფორმაცია რეალურად იკარგება შავ ხვრელებში. ეს ახალი კოსმოლოგიური მოდელი შეიძლება ექსპერიმენტულად შემოწმდეს კოსმოსური მიკროტალღური ფონური გამოსხივების (CMB) დეტალური ანალიზით: თუ სიმართლეა, CMB უნდა ავლენდეს წრიულ ნიმუშებს ოდნავ დაბალი ან ოდნავ მაღალი ტემპერატურით. 2010 წლის ნოემბერში პენროუზმა და ვ.გ. გურზადიანმა განაცხადეს, რომ მათ აღმოაჩინეს ასეთი წრიული ნიმუშების მტკიცებულება უილკინსონის მიკროტალღური ანიზოტროპიის ზონდის (WMAP) მონაცემებში , რაც დადასტურდა BOOMERanG ექსპერიმენტის მონაცემებით . ამ დასკვნების მნიშვნელობა საკამათო იყო.

მსგავსი მიმართულებით, მოდაკი, ორტიზი, პენია და სუდარსკი ამტკიცებდნენ, რომ პარადოქსის გადაჭრა შესაძლებელია კვანტური თეორიის ფუნდამენტური საკითხების მოხმობით, რომლებსაც ხშირად კვანტური მექანიკის გაზომვის პრობლემას უწოდებენ. ეს ნაშრომი ეფუძნება ოკონისა და სუდარსკის ადრინდელ წინადადებას ობიექტური კოლაფსის თეორიის სარგებლის შესახებ გაცილებით ფართო კონტექსტში. ამ კვლევების თავდაპირველი მოტივაცია იყო პენროუზის დიდი ხნის წინადადება, რომლის მიხედვითაც ტალღური ფუნქციის კოლაფსი გარდაუვალია შავი ხვრელების არსებობისას (და გრავიტაციული ველის გავლენის ქვეშაც კი). კოლაფსის თეორიების ექსპერიმენტული დადასტურება მიმდინარე ძალისხმევაა.

სხვა შემოთავაზებული რეზოლუციები

პარადოქსის გადაჭრის სხვა გზებიც იქნა შესწავლილი. ისინი მოკლედ არის ჩამოთვლილი ქვემოთინფორმაცია ინახება დიდ ნარჩენად

ეს იდეა იმაზე მიუთითებს, რომ ჰოკინგის გამოსხივება წყდება მანამ, სანამ შავი ხვრელი პლანკის ზომას მიაღწევს. რადგან შავი ხვრელი არასდროს აორთქლდება, მისი საწყისი მდგომარეობის შესახებ ინფორმაცია შეიძლება შავი ხვრელის შიგნით დარჩეს და პარადოქსი ქრება. თუმცა, არ არსებობს მიღებული მექანიზმი, რომელიც ჰოკინგის გამოსხივების შეჩერებას საშუალებას მისცემს, სანამ შავი ხვრელი მაკროსკოპული რჩება.
ინფორმაცია ინახება ახალშობილ სამყაროში, რომელიც ჩვენი სამყაროსგან გამოყოფილია.
გრავიტაციის ზოგიერთი მოდელი, როგორიცაა აინშტაინ-კარტანის გრავიტაციის თეორია, რომელიც ზოგადი ფარდობითობის თეორიას შინაგანი კუთხური იმპულსის ( სპინის ) მქონე მატერიაზე აფართოებს, ასეთი პატარა სამყაროების ფორმირებას წინასწარმეტყველებს. ფიზიკის ცნობილი ზოგადი პრინციპების დარღვევა საჭირო არ არის. სამყაროების რაოდენობაზე ფიზიკური შეზღუდვები არ არსებობს, მიუხედავად იმისა, რომ მხოლოდ ერთი რჩება დაკვირვებადი.
აინშტაინ-კარტანის თეორიის შემოწმება რთულია, რადგან მისი პროგნოზები მნიშვნელოვნად განსხვავდება ზოგად-რელატივისტური პროგნოზებისგან მხოლოდ უკიდურესად მაღალი სიმკვრივის შემთხვევაში.
ინფორმაცია კოდირებულია მომავალსა და წარსულს შორის კორელაციებით
საბოლოო მდგომარეობის წინადადება გვთავაზობს, რომ შავი ხვრელის სინგულარობაზე სასაზღვრო პირობები უნდა დაწესდეს, რაც, მიზეზობრივი პერსპექტივიდან გამომდინარე, შავი ხვრელის ინტერიერში ყველა მოვლენის მომავალს ეხება. ეს ხელს უწყობს შავი ხვრელის აორთქლების უნიტარულობასთან შეთავსებას, მაგრამ ეწინააღმდეგება დროითი ევოლუციის მიზეზობრიობისა და ლოკალურობის ინტუიციურ იდეას.
კვანტური არხის თეორია
2014 წელს კრის ადამიმ ამტკიცებდა, რომ კვანტური არხის თეორიის გამოყენებით ანალიზი ნებისმიერი აშკარა პარადოქსის გაქრობას იწვევს; ადამი უარყოფს შავი ხვრელის კომპლემენტარობას და ამის ნაცვლად ამტკიცებს, რომ არცერთი კოსმოსური ზედაპირი არ შეიცავს დუბლიკატირებულ კვანტურ ინფორმაციას .

იხ,ვიდეო - Hawking's black hole paradox explained - Fabio Pacucci

შოთას ბლოგი

Translate

суббота, 6 сентября 2025 г.

შავი ხვრელის საინფორმაციო პარადოქსი

ცოდნა სინათლეა - Knowledge is light - Знание свет -

შესაბამისი პრინციპები