ცოდნა სინათლეა - Knowledge is light - Знание свет -                                                 მათემატიკის დარგი

                            ტოპოლოგია

მობიუსის ლენტი, ერთმხრიანი ზედაპირი. მსგავსი ფიგურები ხშირად გვხდება ტოპოლლოგიაში

(ბერძნ. topos – ადგილი, logos – სწავლა) — მათემატიკის დარგი, რომლის შესწავლის ობიექტებია ტოპოლოგიური სივრცეები, უწყვეტი ასახვები, და დაკავშირებული მათემატიკური ცნებები. მისი მეშვეობით ხდება მათემატიკაში ისეთი ფუნდამენტური ცნებების ფორმალიზება, როგორიცაა ბმულობა, კრებადობა, უწყვეტობა და ა.შ. მე-20 საუკუნის დასაწყისში დარგის დაარსებისას, მას geometria situs (ლათ. „ადგილის გეომეტრია“) და analysis situs (ლათ. „ადგილის ანალიზი“) უწოდებდნენ. 1925-75 წლებში მატემატიკის განვითარების ყველაზე მნიშვნელოვანი სფერო იყო.

ტოპოლოგიის ერთ-ერთი თეორემა პოპულარულ ენაზე შემდეგნაირად შეიძლება ჩამოყალიბდეს: „შეუძლებელია თმით დაფარული ბურთის მთლიანად გლუვად დავარცხნა“. ეს ინტუიციურად გასაგები ფაქტია. ფორმალურად კი იგივე თეორემა შემდეგში მდგომარეობს: „სფეროზე არ არსებობს არაქრობადი უწყვეტი მხები ვექტორი“, და მისი დამტკიცება არატრივიალურია. ეს თეორემა სამართლიანია არა მარტო სფეროსათვის არამედ ყველა შეკრული ზედაპირისთვის ნახვრეტების გარეშე (გარკვეული პირობების დაკმაყოფილების შემთხვევაში) და უკავშირდება „გეომეტრიული ფიგურების“ გარკვეულ ზოგად თვისებებს. ამ თვისებების გამოკვლევა ტოპოლოგიის საკითხია.

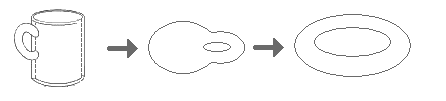
ხშირად ტოპოლოგიას აღწერენ როგორც გეომეტრიის ნაწილს, გეომეტრიული ობიექტების უზოგადესი თვისებების შესახებ, თვისებების რომლებიც უცვლელი რჩება უწყვეტი დეფორმაციების დროს (შეკუმშვა, გაწელვა, მოღუნვა; იხ. ნახატი ქვემოთ). გეომეტრიული ფიგურები, რომლებიც ერთიმეორისგან ამგვარი უწყვეტი დეფორმაციების საშუალებით მიიღება, ტოპოლოგიის თვალსაზრისით არ განსხვავდება (ჰომეომორფიზმი).

ფინჯანი, გირი და ბლითი „ტოპოლოგიურად“ ერთი და იგივე გეომეტრიული ფიგურებია

ალგებრული ტოპოლოგიის ზოგადი მეთოდია სხვადასხვა „გეომეტრიული“ ობიექტებისთვის უფრო გამოთვლადი „ალგებრული“ (დისკრეტული) ინვარიანტების შეთანადება. ამბობენ რომ ალგებრული ტოპოლოგია სწავლობს გეომეტრიას, ალგებრის გამოყენებით. (ტოპოლოგიის სხვადასხვა დარგების შესახებ იხილეთ ქვემოთ).

ტოპოლოგიამ უმთავრესი გავლენა მოახდინა მათემატიკის ისეთ დარგებზე როგორიცაა: ალგებრული გეომეტრია, დიფერენციალური გეომეტრია, დინამიკური სისტემები, დიფერენციალური განტოლებები და სხვ.

                                                                  

ჰოლიჰერდრა (კუბო-ჰემიოლტაჰედრონი)

ტოპოლოგია მოიცავს ერთმანეთისგან საკმაოდ დაშორებულ რამდენიმე ქვედარგს.

• სიმრავლური ტოპოლოგია ანუ ზოგადი ტოპოლოგია იკვლევს ზოგად ტოპოლოგიურ სივრცეებს. მისი პირველი თეორემები შეეხება ტოპოლოგიური სივრცეების ფუნდამენტურ თვისებებს (იხ. ქვემოთ), რომლებიც მნიშვნელოვანია მათემატიკის სხვა ნაწილებში. სიმრავლური ტოპოლოგია თანამედროვე მათემატიკური ანალიზის სტანდარტული საფუძველია.

• ალგებრულ ტოპოლოგიაში შეისწავლება უფრო ვიწრო ტოპოლოგიური სივრცეების კლასები, მაგალითად პოლიჰედრები და CW კომპლექსები. დარგი ინტენსიურად იყენებს აბსტრაქტულ ალგებრას. მე-20 საუკუნის მეორე ნახევრიდან მასზე გავლენა იქონია კატეგორიათა თეორიამ (იხ. წარმოუბული ფუნქტორი, სიმპლიციალური სიმრავლე). თავის მხრივ, ალგებრული ტოპოლოგიის იდეებს გავლენა აქვთ ალგებრულ გეომეტრიაზე, ალგებრასა და კატეგორიათა თეორიაზე. ალგებრულმა ტოპოლოგიამ თანამედროვე მათემატიკაში შემოიტანა ისეთი მნიშვნელოვანი ცნებები, როგორიცაა: დამფარავი ასახვა, ფიბრაცია, ფუნდამენტური ჯგუფი, ჰომოტოპია, ჰომოლოგია, კოჰომოლოგია, სპექტრალური მიმდევრობა.
•                                                                
  
• კვანძების თეორია ტოპოლოგიის ქვედარგი

• ტოპოლოგიის კიდევ ერთი ვრცელი დარგი დიფერენციალური ტოპოლოგია იკვლევს აბსტრაქტულ დიფერენციალურ სტრუქტურებს, ეს მოიცავს: დიფერენციალურ მრავალნაირობებს, დიფერენციალურ ფორმებს და ა.შ. ისტორიულად იგი აღმოცენდა დიფერენციალური განტოლებების შესწავლიდან. დიფერენციალური ტოპოლოგიის ცნობილი სტოქსის თეორემა არის ანალიზის ფუნდამენტური თეორემის განზოგადება დიფერენციალური ფორმებისთვის.

ტოპოლოგიის სხვა მიმართულებებია, მაგალითად, კვანძების თეორია, (კო)ბორდიზმების თეორია, ტოპოლოგიური K-თეორია და სხვ.

იხ. ვიდეო პროფესორი ივანე წერეთელი - ლექციის თემა "ტოპოლოგია" - 

ვიდეო ლექციაში საუბარია თანამედროვე მათემატიკის ერთ-ერთ უმნიშვნელოვანეს დარგზე - ტოპოლოგიაზე. კერძოდ,  გადმოცემულია მოკლე პრეისტორია და ის ძირითადი იდეები, რომლებზე დაყრდნობითაც ტოპოლოგია ჩამოყალიბდა.

• ტიხონოვის თეორემა: კომპაქტური სივრცეების ნამრავლი კომპაქტურია.

• თეორემები უძრავი წერტილის შესახებ გამოიყენება დიფერენციალური განტოლებების ამოსახსნელად.

• ტიცეს გაფართოების თეორემა: ნორმალური სივრცის ნებისმიერ ჩაკეტილ ქვესიმრავლეზე განმარტებული ნამდვილი უწყვეტი ფუნქცია შეიძლება გავრცელდეს მთელ სივრცეზე.

• მეტრიზაციის თეორემები იძლევა ტოპოლოგიური სივრცის მეტრიზებადობის აუცილებელ და საკმარის პირობებს.

• ბერის კატეგორიის თეორემა: თუ X სრული მეტრიკული სივრცეა ან ლოკალურად კომპაქტური ჰაუსდორფის სივრცე, მაშინ მისი არსადმკვრივი ქვესიმრავლეების ნებისმიერი თვლადი გაერთიანების ბირთვი ცარიელია.

უფრო ზოგადი თეორიები

შედეგების ანალიზს და შემდგომ მათემატიკურ აბსტრაგირებას მივყავართ უფრო ზოგადი სტრუქტურების კვლევისკენ. უწერტილო ტოპოლოგია სწავლობს ტოპოლოგიურ სივრცეებთან დაკავშირებულ თვისებებს კიდევ უფრო ზოგად სიტუაციებში. თავდაპირველად ტოპოლოგიაში გაჩენილმა იდეებმა აგრეთვე განვითარება ჰპოვა კატეგორიათა თეორიის სხვადასხვა კონტექსტში.