მოვლენათა ჰორიზონტი

ცოდნა სინათლეა - Knowledge is light - Знание свет -  

                 მოვლენათა ჰორიზონტი

მოვლენათა ჰორიზონტი ასტროფიზიკაში საზღვარია, რომლის იქითაც მოვლენებს დამკვირვებელზე გავლენის მოხდენა არ შეუძლიათ.

ეს ტერმინი შემოიღო ვოლფგანგ რინდლერმა  .

1784 წელს ჯონ მიჩელმა ივარაუდა, რომ კომპაქტურ მასიურ ობიექტებთან ახლოს გრავიტაცია შესაძლოა იმდენად ძლიერი ყოფილიყო, რომ სინათლეც კი ვერ გადალახავდა მას. იმ დროს დომინანტური თეორიები იყო ნიუტონის გრავიტაცია და ე.წ. სინათლის კორპუსკულური თეორია . ამ თეორიების თანახმად, თუ ობიექტის გაქცევის სიჩქარე აღემატება სინათლის სიჩქარეს, მისგან გამოქცეული სინათლე შეიძლება დროებით გადაადგილდეს, მაგრამ საბოლოოდ დაბრუნდეს. 1958 წელს დევიდ ფინკელშტეინმა გამოიყენა ზოგადი ფარდობითობა , რათა შემოეტანა შავი ხვრელის ლოკალური მოვლენების ჰორიზონტის უფრო მკაცრი განმარტება , როგორც საზღვარი, რომლის მიღმაც ნებისმიერი სახის მოვლენას არ შეუძლია გავლენა მოახდინოს გარე დამკვირვებელზე. ამან გამოიწვია ინფორმაციული პარადოქსი და ფაირვოლური პარადოქსი , რამაც გამოიწვია ლოკალური მოვლენების ჰორიზონტების კონცეფციისა და შავი ხვრელის ცნების გადახედვა. შემდგომში შემუშავდა რამდენიმე თეორია, როგორც მოვლენათა ჰორიზონტით, ასევე მის გარეშე. სტივენ ჰოკინგმა , რომელიც შავი ხვრელების აღმწერი თეორიების ერთ-ერთი წამყვანი შემქმნელი იყო, შესთავაზა მოვლენათა ჰორიზონტის ნაცვლად ხილული ჰორიზონტის  და განაცხადა, რომ „გრავიტაციული კოლაფსი ქმნის ხილულ ჰორიზონტებს და არა მოვლენათა ჰორიზონტებს“. საბოლოოდ მან დაასკვნა, რომ „მოვლენათა ჰორიზონტის არარსებობა ნიშნავს შავი ხვრელების არარსებობას — იმ სტრუქტურების გაგებით, საიდანაც სინათლეს უსასრულობაში გაქცევა არ შეუძლია“.  ეს არ ნიშნავს, რომ შავი ხვრელები არ არსებობს, ეს უბრალოდ გამოხატავს უნდობლობას მოვლენათა ჰორიზონტის ტრადიციული მკაცრი განმარტების მიმართ . 

დამკვირვებლის პერსპექტივიდან ჰორიზონტთან მიახლოებული ნებისმიერი ობიექტი თითქოს შენელდება და ჰორიზონტს სრულად ვერასდროს კვეთს  . გრავიტაციული წითელი წანაცვლების გამო , ჰორიზონტთან მიახლოებისას მისი გამოსახულება დროთა განმავლობაში უფრო წითელი და მკრთალი ხდება  .

გაფართოებად სამყაროში გაფართოების სიჩქარე აღწევს და აღემატება კიდეც სინათლის სიჩქარეს, რაც ხელს უშლის სიგნალებს ზოგიერთ რეგიონამდე მიღწევაში. კოსმოსური მოვლენათა ჰორიზონტი რეალური მოვლენათა ჰორიზონტია, რადგან ის გავლენას ახდენს ყველა სახის სიგნალზე, მათ შორის გრავიტაციულ ტალღებზე , რომლებიც სინათლის სიჩქარით მოძრაობენ.

ჰორიზონტების უფრო სპეციფიკური ტიპები მოიცავს შავი ხვრელების გარშემო არსებულ დაკავშირებულ, მაგრამ განსხვავებულ ხილულ და ^{აბსოლუტურ} ჰორიზონტებს . სხვა განსხვავებული ტიპებია კოშისა და კილინგის ჰორიზონტები ; ფოტონის სფეროები და კერის ხსნარის ერგოსფეროები ; ნაწილაკური და კოსმოლოგიური ჰორიზონტები , რომლებიც მნიშვნელოვანია კოსმოლოგიისთვის ; და იზოლირებული და ^{დინამიური} ჰორიზონტები , რომლებიც მნიშვნელოვანია შავი ხვრელების თანამედროვე კვლევაში.

კოსმოსური მოვლენების ჰორიზონტი

კოსმოლოგიაში , დაკვირვებადი სამყაროს მოვლენათა ჰორიზონტი არის უდიდესი თანამოძრაობის მანძილი , საიდანაც ახლა გამოსხივებულ სინათლეს შეუძლია მომავალში დამკვირვებელამდე მიაღწიოს. ის განსხვავდება ნაწილაკების ჰორიზონტისგან, რომელიც არის უდიდესი თანამოძრაობის მანძილი, საიდანაც წარსულში გამოსხივებულ სინათლეს შეუძლია დამკვირვებელამდე მიაღწიოს აწმყოში. ამ მანძილის მიღმა მომხდარი მოვლენებისთვის, სინათლეს არ აქვს საკმარისი დრო ჩვენს ადგილმდებარეობამდე მისასვლელად, მაშინაც კი, თუ ის სამყაროს დასაწყისშივე იყო გამოსხივებული. ნაწილაკების ჰორიზონტის ევოლუცია დროთა განმავლობაში დამოკიდებულია სამყაროს გაფართოების ბუნებაზე . გაფართოების ზოგიერთი მახასიათებლისთვის, სამყაროს იქნება ნაწილები, რომლებიც არასდროს დაკვირვებადი იქნება, მიუხედავად იმისა, თუ რამდენ ხანს დაელოდება დამკვირვებელი სინათლის მოსვლას ამ რეგიონებიდან. საზღვარი, რომლის მიღმაც მოვლენები არასდროს დაკვირვებადი იქნება, არის მოვლენათა ჰორიზონტი და ის წარმოადგენს ნაწილაკების ჰორიზონტის მაქსიმალურ სიგრძეს.

სამყაროსთვის ნაწილაკების ჰორიზონტის არსებობის დადგენის კრიტერიუმი შემდეგია. ჩვენ შემოგვაქვს თანამოძრაების მანძილი d _p , როგორც

${\displaystyle {\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">დ</span></span>}}_{\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">გვ</span></span>}}<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">=</span></span>{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">\int </span></span>}_{\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">0</span></span>}}^{{\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">ტ</span></span>}}_{\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">0</span></span>}}}\frac{\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">გ</span></span>}}{\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">ა</span></span>}<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">(</span></span>\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">ტ</span></span>}<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">)</span></span>}\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">დ</span></span>}\mathrm{<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">ტ</span></span>}<span\; style="vertical-align:\; inherit;"><span\; style="vertical-align:\; inherit;">.</span></span>}$

ამ განტოლებაში , a არის მასშტაბის კოეფიციენტი , c არის სინათლის სიჩქარე და t ₀ არის სამყაროს ასაკი. თუ d _p → ∞ (ანუ წერტილები თვითნებურად არის დაშორებული, რაც შეიძლება შორს დაკვირვებისთვის), მაშინ მოვლენათა ჰორიზონტი არ არსებობს. თუ d _p ≠ ∞ , მაშინ ჰორიზონტი არსებობს.

მოვლენათა ჰორიზონტის გარეშე კოსმოლოგიური მოდელების მაგალითებია სამყაროები, რომლებშიც დომინირებს მატერია ან რადიაცია . მოვლენათა ჰორიზონტის მქონე კოსმოლოგიური მოდელის მაგალითია სამყარო, რომელსაც დომინირებს კოსმოლოგიური მუდმივა ( დე სიტერის სამყარო ).

კოსმოლოგიური მოვლენათა ჰორიზონტებისა და ნაწილაკების სიჩქარეების გამოთვლა მოცემულია ფრიდმანის კოსმოლოგიური მოდელის შესახებ სტატიაში , რომელშიც სამყარო დაახლოებით წარმოდგენილია, როგორც არაურთიერთქმედებადი კომპონენტებისგან შემდგარი, რომელთაგან თითოეული იდეალური სითხეა  .

შავი ხვრელის მოვლენათა ჰორიზონტი

 

შავი ხვრელისგან შორს, ნაწილაკებს შეუძლიათ ნებისმიერი მიმართულებით გადაადგილება, რაც შემოიფარგლება მხოლოდ სინათლის სიჩქარით.

შავ ხვრელთან უფრო ახლოს, სივრცე-დრო იწყებს გამრუდებას. ზოგიერთ კოორდინატთა სისტემაში შავი ხვრელისკენ მიმავალი გზა უფრო მეტია, ვიდრე შავი ხვრელიდან გასასვლელი.

მოვლენათა ჰორიზონტის შიგნით, ყველა გზა ნაწილაკებს შავი ხვრელის ცენტრში მიჰყავს. ნაწილაკებს შავი ხვრელიდან თავის დაღწევის საშუალება არ აქვთ.

მოვლენათა ჰორიზონტის ერთ-ერთი ყველაზე ცნობილი მაგალითი ზოგადი ფარდობითობის თეორიაში შავი ხვრელის აღწერაშია მოცემული. შავი ხვრელი არის კოსმოსური ობიექტი, რომელიც იმდენად მკვრივია, რომ ახლომდებარე მატერიას ან რადიაციას არ შეუძლია მისი გრავიტაციული ველიდან გამოსვლა . ეს ხშირად აღწერილია, როგორც საზღვარი, რომლის ფარგლებშიც შავი ხვრელის გაქცევის სიჩქარე აღემატება სინათლის სიჩქარეს . თუმცა, უფრო დეტალური აღწერა ის არის, რომ ამ ჰორიზონტის ფარგლებში, ყველა სინათლის მსგავსი გზა (გზები, რომელთა გავლაც სინათლეს შეუძლია) და შესაბამისად, ყველა ნაწილაკის გზა ჰორიზონტის შიგნით მომავალი სინათლის კონუსების სახითაა მოხრილი , ისე, რომ ისინი შავ ხვრელში მიდიან. როგორც კი ნაწილაკი ჰორიზონტში მოხვდება, შავ ხვრელში გადაადგილება ისეთივე გარდაუვალია, როგორც დროში წინსვლა - მიუხედავად იმისა, თუ რომელი მიმართულებით მოძრაობს ნაწილაკი. ეს მოძრაობები შეიძლება განვიხილოთ, როგორც ერთმანეთის ეკვივალენტური, გამოყენებული სივრცე-დროის კოორდინატთა სისტემის მიხედვით  .

შესაძლოა, შავი ხვრელიდან ენერგია გამოვიდეს ე.წ. ჰოკინგის გამოსხივების გზით, რაც კვანტური ეფექტია. თუ ასეა, ჩვენს სამყაროში არსებული კოლაფსირებული ობიექტებისთვის რეალური მოვლენათა ჰორიზონტები მკაცრი გაგებით არ ყალიბდება . თუმცა, რადგან ასტროფიზიკური კოლაფსირებული ობიექტები კლასიკური სისტემებია, კლასიკური შავი ხვრელის მოდელით მათი აღწერის სიზუსტე საკმარისია ყველა შესაძლო ასტროფიზიკური გამოყენებისთვის  .

შვარცშილდის რადიუსით განსაზღვრული ზედაპირი მოქმედებს როგორც ამ რადიუსში მოქცეული არამბრუნავი სხეულის მოვლენათა ჰორიზონტი (თუმცა მბრუნავი შავი ხვრელი გარკვეულწილად განსხვავებულად მუშაობს). ობიექტის შვარცშილდის რადიუსი მისი მასის პროპორციულია. თეორიულად, მატერიის ნებისმიერი რაოდენობა შავ ხვრელად იქცევა, თუ ეს მატერია შეკუმშულია მოცულობაში, რომელიც შეესაბამება შვარცშილდის შესაბამის რადიუსს. მზის მასისთვის ეს რადიუსი დაახლოებით 3 კილომეტრია, ხოლო დედამიწისთვის - დაახლოებით 9 მილიმეტრი. თუმცა, პრაქტიკაში არც დედამიწას და არც მზეს არ აქვთ საჭირო მასა და შესაბამისად, აუცილებელი გრავიტაციული ძალა, რათა გადალახონ გადაგვარებული ელექტრონისა ^და ნეიტრონული აირის წნევა . ვარსკვლავის ამ წნევის მიღმა კოლაფსისთვის საჭირო მინიმალური მასა შეესაბამება ოპენჰაიმერ-ვოლკოფის ზღვარს , რომელიც დაახლოებით სამი მზის მასაა.

^{გრავიტაციული კოლაფსის ფუნდამენტური მოდელების}  მიხედვით ^, მოვლენათა ჰორიზონტი შავი ხვრელის სინგულარობამდე ყალიბდება. თუ ირმის ნახტომის ყველა ვარსკვლავი თანდათანობით დაჯგუფდება გალაქტიკის ცენტრში, ერთმანეთისგან პროპორციული მანძილის შენარჩუნებით, ისინი ყველა თავიანთ საერთო შვარცშილდის რადიუსში მოხვდებიან შეჯახებამდე დიდი ხნით ადრე  . მოვლენათა ჰორიზონტით გარშემორტყმულ გალაქტიკაში დამკვირვებლები ჩვეულებრივად იცხოვრებენ შორეულ მომავალში კოლაფსამდე.

შავი ხვრელის მოვლენათა ჰორიზონტთან დაკავშირებით ფართოდ გავრცელებული მცდარი წარმოდგენა არსებობს. გავრცელებული, თუმცა მცდარი მოსაზრებაა, რომ შავი ხვრელები მატერიას გარემოდან „იწოვენ“, სინამდვილეში კი ისინი მატერიას შთანთქავენ ნებისმიერი სხვა გრავიტაციული სხეულის მსგავსად, რადგან ობიექტის შავ ხვრელად გადაქცევის შემდეგ მისი გრავიტაციული ველი არ გაზრდილა. კიდევ ერთი საკითხია ის, რომ ის ახლა გაცილებით მცირე მოცულობიდან მოდის და ძლიერად არის მოხრილი. ეს ასევე საშუალებას აძლევს მატერიას (მაგალითად, გაზს) მიუახლოვდეს ცენტრს და მიაღწიოს მაღალ სიჩქარეს მის გარშემო ბრუნვისას. არანაკლებ გავრცელებულია მოსაზრება, რომ მატერიის დაკვირვება შესაძლებელია შავ ხვრელში. ეს სიმართლეს არ შეესაბამება. პოტენციურად, შავი ხვრელის გარშემო მხოლოდ აკრეციული დისკის , რომელშიც მატერია ისეთი სიჩქარით მოძრაობს, რომ ხახუნი ქმნის მაღალი ენერგიის გამოსხივებას, რომლის დაკვირვებაც შესაძლებელია (როდესაც მატერიის ნაწილი გამოიდევნება აკრეციული დისკიდან შავი ხვრელის ბრუნვის ღერძის გასწვრივ, ქმნის ხილულ ჭავლებს მატერიასთან, როგორიცაა ვარსკვლავთშორისი აირი, ურთიერთქმედებისას ან როდესაც მისი ბრუნვის ღერძი პირდაპირ დედამიწისკენ არის მიმართული). უფრო მეტიც, შორეული დამკვირვებელი ვერასდროს დაინახავდა ჰორიზონტამდე რაიმეს მიღწევას. მათთვის, როგორც ჩანს, ობიექტის სიჩქარე უსასრულოდ მცირდებოდა შავ ხვრელთან მიახლოებისას, ხოლო ობიექტის მიერ გამოსხივებული სინათლე სულ უფრო და უფრო წითელი გახდებოდა.

შავი ხვრელის მოვლენათა ჰორიზონტი ტელეოლოგიური ხასიათისაა, რაც იმას ნიშნავს, რომ ჰორიზონტის მიმდინარე პოზიციის დასადგენად სამყაროს მთელი მომავალი სივრცე-დროის ცოდნა დაგვჭირდება, რაც არსებითად შეუძლებელია. მოვლენათა ჰორიზონტის საზღვრის წმინდა თეორიული ბუნების გამო, მოძრავი ობიექტი აუცილებლად არ განიცდის უცნაურ ეფექტებს და რეალურად გადის გამოთვლილ საზღვარს სასრულ საკუთარ დროში  .

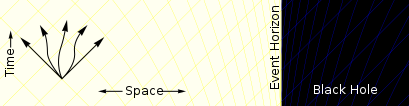
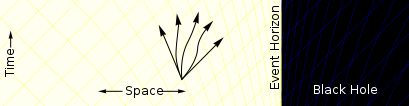
აჩქარებული ნაწილაკის აშკარა ჰორიზონტი

სივრცე-დროის დიაგრამა, რომელიც ასახავს ერთგვაროვნად აჩქარებულ ნაწილაკს, P-ს , და მოვლენა E-ს , რომელიც ნაწილაკის ხილული ჰორიზონტის მიღმაა. მოვლენის E სინათლის კონუსის ზედა ნაწილი არასდროს კვეთს ნაწილაკის სამყაროს ხაზს .

თუ ნაწილაკი გრავიტაციული ველებისგან თავისუფალ არაგაფართოებულ სამყაროში მუდმივი სიჩქარით მოძრაობს, მაშინ ამ სამყაროში მომხდარ ნებისმიერ მოვლენას საბოლოოდ ნაწილაკი დააკვირდება, რადგან ამ მოვლენებიდან მომავალი სინათლის კონუსი ნაწილაკის სამყაროს ხაზს კვეთს. მეორეს მხრივ, თუ ნაწილაკი აჩქარებს, მაშინ ზოგიერთ სიტუაციაში ზოგიერთი მოვლენიდან სინათლის კონუსები არასდროს კვეთენ ნაწილაკის სამყაროს ხაზს. ამ პირობებში ^, აჩქარებული ნაწილაკის ათვლის სისტემას აქვს ხილული ჰორიზონტი , რომელიც წარმოადგენს საზღვარს, რომლის მიღმაც მოვლენები დაკვირვებადი არ არის.

ამ სიტუაციის სივრცე-დროის დიაგრამა ნაჩვენებია მარჯვენა მხარეს მოცემულ ფიგურაზე. ნაწილაკის აჩქარებისას ის უახლოვდება, მაგრამ ვერასდროს აღწევს, სინათლის სიჩქარეს თავისი საწყისი ათვლის სისტემასთან მიმართებაში. სივრცე-დროის დიაგრამაზე მისი გზა ჰიპერბოლაა , რომელიც ასიმპტოტურად უახლოვდება 45-გრადუსიან ხაზს (სინათლის სხივის გზა). მოვლენა, რომლის სინათლის კონუსის საზღვარიც ეს ასიმპტოტაა, ან ნებისმიერი მოვლენა ამ საზღვრის მიღმა, ვერასდროს დაიკვირვება აჩქარებული ნაწილაკის მიერ. ნაწილაკის ათვლის სისტემაში არსებობს საზღვარი, რომლის იქითაც ვერანაირი სიგნალი ვერ გავა (ხილული ჰორიზონტი).

მიუხედავად იმისა, რომ ამ ტიპის მიახლოებები შეიძლება მოხდეს რეალურ სამყაროში (მაგ., ნაწილაკების ამაჩქარებელში ), ამ ტიპის რეალური მოვლენათა ჰორიზონტი არ არსებობს, რადგან ის მოითხოვს ნაწილაკს, რომელიც განუსაზღვრელი ვადით უნდა აჩქარდეს (რაც მოითხოვს ენერგიის უსასრულო რაოდენობას).

მოვლენათა ჰორიზონტების სხვა მაგალითები

• მინკოვსკის სივრცეში მუდმივი საკუთარი აჩქარებით მოძრავი დამკვირვებლისთვის (მისი სიჩქარე ინერციულ ათვლის სისტემაში უახლოვდება სინათლის სიჩქარეს, მაგრამ არ აღწევს მას), არსებობს ორი მოვლენათა ჰორიზონტი, ე.წ. რინდლერის ჰორიზონტები (იხ. რინდლერის კოორდინატები ). გარდა ამისა, აჩქარებული დამკვირვებლისთვის არსებობს ჰოკინგის გამოსხივების ანალოგი  - უნრუჰის გამოსხივება .
  
• თუ თანამედროვე კოსმოლოგიური მოდელი Λ-CDM სწორია, ჩვენს სამყაროში მომავალი მოვლენათა ჰორიზონტი არსებობს .
• აკუსტიკაში ასევე არსებობს ურთიერთქმედების გავრცელების სასრული სიჩქარე - ხმის სიჩქარე , რის გამოც აკუსტიკისა და ფარდობითობის თეორიის მათემატიკური აპარატურა და ფიზიკური შედეგები ანალოგიური ხდება, ხოლო სითხის ან გაზის ზებგერითი ნაკადების დროს წარმოიქმნება მოვლენების ჰორიზონტების ანალოგები - აკუსტიკური ჰორიზონტები.

ურთიერთქმედება მოვლენათა ჰორიზონტთან

მოვლენათა ჰორიზონტისკენ მიმართული ობიექტები გამგზავნი დამკვირვებლის თვალსაზრისით მას არასდროს კვეთენ (რადგან ჰორიზონტის გადამკვეთი მოვლენის სინათლის კონუსი არასდროს კვეთს დამკვირვებლის სამყაროს ხაზს ). ჰორიზონტთან ახლოს მდებარე ობიექტის დამკვირვებელთან შედარებით უმოძრაოდ შენარჩუნების მცდელობა უზარმაზარი ძალების გამოყენებას მოითხოვს. რაც უფრო ახლოსაა ჰორიზონტთან, მით უფრო დიდია ასეთი ძალის სიდიდე, რომელიც ზღვარზე უსაზღვროდ იზრდება (უსასრულო ხდება).

ცარიელ სივრცეში ერთნაირად აჩქარებული დამკვირვებლის მიერ აღქმული ჰორიზონტის შემთხვევაში, ჰორიზონტი დამკვირვებლისგან ფიქსირებულ მანძილზე რჩება მიუხედავად იმისა, თუ როგორ მოძრაობს გარემო. დამკვირვებლის აჩქარების ცვლილებამ შეიძლება გამოიწვიოს ჰორიზონტის დროთა განმავლობაში გადაადგილება ან ხელი შეუშალოს მოვლენათა ჰორიზონტის არსებობას, არჩეული აჩქარების ფუნქციის მიხედვით. დამკვირვებელი არასდროს ეხება ჰორიზონტს და არასდროს კვეთს მას.

დე სიტერის სამყაროს მკვიდრის მიერ აღქმული ჰორიზონტის შემთხვევაში , ჰორიზონტი ინერციული დამკვირვებლისგან ფიქსირებულ მანძილზეა . აჩქარებადი დამკვირვებელიც კი არასდროს შედის მასთან კონტაქტში.

რაც შეეხება შავი ხვრელის გარშემო მოვლენათა ჰორიზონტს, ობიექტის მიმართ ყველა შორეული დამკვირვებელი, რომელიც სტაციონარულია, თანხმდება მის მდებარეობაზე. მიუხედავად იმისა, რომ პრინციპში, დამკვირვებლისთვის შესაძლებელი იქნებოდა შავი ხვრელისკენ თოკით (ან ღეროთი) პირდაპირ მის ჰორიზონტთან გადაადგილება, პრაქტიკაში ეს შეუძლებელია. ჰორიზონტამდე სათანადო მანძილი სასრულია  , ამიტომ საჭირო თოკის სიგრძეც სასრულია, მაგრამ თუ თოკს ნელა დავეშვებით (ისე, რომ მასზე თითოეული წერტილი შვარცშილდის კოორდინატებში იყოს უძრავ მდგომარეობაში), სათანადო აჩქარება ( g ), რომელსაც განიცდიან თოკზე ჰორიზონტთან უფრო ახლოს მდებარე წერტილები, უსასრულობისკენ მიისწრაფვის, ამიტომ თოკი გაწყდება. თუ თოკს სწრაფად დავეშვებით (შესაძლოა თავისუფალი ვარდნის დროსაც კი), მაშინ დამკვირვებელი, რომელიც მის ბოლოებს ჩაეჭიდება, მართლაც შეძლებს მოვლენათა ჰორიზონტამდე მისვლას და მის გადაკვეთასაც კი. თუმცა, შეუძლებელი იქნება თოკის ბოლოს გამოწევა მოვლენათა ჰორიზონტის უკნიდან. გაჭიმული თოკის გასწვრივ მოქმედი ძალები განუსაზღვრელი ვადით გაიზრდება, როდესაც ისინი მოვლენათა ჰორიზონტს მიუახლოვდებიან და გარკვეულ მომენტში თოკი გაწყდება. უფრო მეტიც, წყვეტა დაფიქსირდება არა მოვლენათა ჰორიზონტზე, არამედ მის წინ, იმ წერტილში, სადაც გარე დამკვირვებელს შეეძლება ამ წყვეტის დაკვირვება.

შავი ხვრელის მოვლენათა ჰორიზონტის გადამკვეთ დამკვირვებლებს შეუძლიათ გამოთვალონ მისი გადაკვეთის მომენტი, მაგრამ თავად ვერაფერ განსაკუთრებულს ვერ დააფიქსირებენ ან ვერ დააკვირდებიან. ვიზუალურად, შავ ხვრელში ჩავარდნილი დამკვირვებლები მოვლენათა ჰორიზონტს აღიქვამენ, როგორც გაუმჭვირვალე შავ რეგიონს მათ ქვემოთ, გრავიტაციული სინგულარობის გარშემო  . სხვა ობიექტები, რომლებიც ჰორიზონტისკენ მოძრაობენ იმავე რადიალური ტრაექტორიით, მაგრამ უფრო ადრეულ დროს, დამკვირვებლის ქვემოთ იქნებიან, მაგრამ მაინც ჰორიზონტის ვიზუალური პოზიციის ზემოთ და თუ მათი ხვრელში ჩავარდნა ძალიან ცოტა ხნის წინ მოხდა, დამკვირვებელი შეძლებდა მათთან შეტყობინებების გაცვლას, სანამ ისინი სინგულარობასთან მიახლოების პროცესში განადგურდებიან  . ადგილობრივად შესამჩნევი ეფექტებია მოქცევითი ძალების დაგროვება და შავი ხვრელის სინგულარობის გავლენა. მოქცევითი ძალები შავი ხვრელის მასის ფუნქციაა. რეალურ ვარსკვლავურ მასის შავ ხვრელში სპაგეტიფიკაცია ადრეულ ეტაპზე ხდება: მოქცევითი ძალები მატერიას ანადგურებენ მოვლენათა ჰორიზონტამდე მიღწევამდე. თუმცა, სუპერმასიურ შავ ხვრელებში , როგორიცაა გალაქტიკების ცენტრში არსებული შავი ხვრელები, სპაგეტიფიკაცია ხდება მოვლენათა ჰორიზონტში. ასტრონავტი მოვლენათა ჰორიზონტზე გავლისას მხოლოდ იმ შემთხვევაში გადარჩება, თუ დაახლოებით 10 000 მზის მასაზე მეტი მასის მქონე შავ ხვრელში მოხვდება.

იხ.ვიდეო - 🧪🧪Горизонт событий, детальный гайд.